T-Test für abhängige Stichproben

Werden  Beobachtungen paarweise einander zugeordnet, so spricht  man von  zwei abhängigen Stichproben. Werden beispielsweise pro  Versuchsperson jeweils zweimal die Reaktionszeiten gemessen,  einmal vor und einmal nach Verabreichung eines Medikaments, so sind  die beiden Messungen abhängige Stichproben. Abhängige Stichproben haben wir aber auch im Falle von parallelen Messungen bei Ehepaaren. Denn auch in diesem Falle können wir einen wechselseitigen Einfluß der paarweise zugeordneten Messungen nicht ausschließen. Die Vorgangsweise sei an einem Beispiel erläutert:

Ausgangsdaten:

Reaktionszeit vorher	Reaktionszeit nachher	di
105	110	-5	0
110	110	0	25
105	110	-5	0
105	115	-10	25
100	110	-10	25
105	105	0	25

Vorgangsweise:

1) Wir berechnen den Mittelwert der Differenzen: 

= -30 / 6 = -5

2)  Unsere Kennwertverteilung ist in diesem Falle die  Verteilung der  Mittelwerte von Differenzen (und nicht - wie im Falle  unabhängiger  Stichproben -: die Verteilung der Differenzen der  Mittelwerte)

Wir  erwarten uns in dieser Verteilung  einen  durchschnittlichen Mittelwert von 0

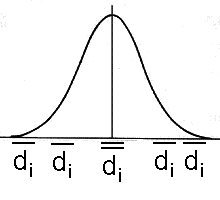
Die  Frage ist nun, wie wahrscheinlich es ist, unter Annahme  der Nullhypothese  (dass  zwischen beiden Messungen  tatsächlich  kein Unterschied besteht), eine Abweichung von -5 zu bekommen.

3) Wir verwenden wiederum die t-Transformation, also:

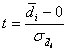
4)  Wir  berechnen . Dies ist der Standardfehler  der  Verteilung  der Mittelwerte von Differenzen:

a)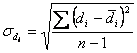

=

Dies ist die geschätzte Standardabweichung der Differenzen.

b)  Der  Standardfehler der Mittelwerte  dieser  Differenzen  ist dann:

5) Daraus ergibt sich folgendes t_errechnet :

6)  Zur  Festlegung von t_kritisch auf  dem  5%  Signifikanzniveau benötigen  wir  vorerst die Freiheitsgrade. Bei  zwei  abhängigen Stichproben sind dies: n - 1, in unserem Beispiel also: 6 -1 = 5

Bei  zweiseitiger  Hypothesenprüfung erhalten wir  ein  t_kritisch von: 2,571

Da  der  Absolutbetrag von t_errechnet größer ist  als  t_kritisch, entscheiden wir uns für die H₁!