Mann-Whitney-U-Test für zwei unabhängige Stichproben

Wir haben bis jetzt einen einzigen Test für unabhängige Stichproben kennen gelernt, nämlich den T-Test. Wie wir bereits wissen, sind an die Berechnung eines T-Tests einige Bedingungen geknüpft. Fassen wir sie kurz zusammen:

Wir berechnen zunächst für beide Stichproben getrennt jeweils einen Stichprobenmittelwert. Die inferenzstatistische Frage lautet dann: Wie wahrscheinlich ist es, folgen wir der Nullhypothese (derzufolge zwischen den Bedingungen unter denen die beiden Stichproben erhoben wurden kein Unterschied besteht) eine solche Mittelwertsdifferenz oder eine gar noch größere zu bekommen?

Um diese Frage in dieser Form aber überhaupt stellen zu können, muss folgendes gegeben sein: 1) Die Daten müssen intervallskaliert sein (denn andernfalls können wir keine Mittelwertsdifferenz berechnen) 2) Die Kennwertverteilung der Mittelwertsdifferenzen ist t-verteilt. Dies ist bei Stichproben mit kleinerem Umfang aber nur dann der Fall, wenn die Daten normalverteilt sind. 3) Die Varianzen in den beiden Stichproben sollten homogen sein. Diese letztere Bedingung wiegt allerdings weniger schwer, wenn wir in beiden Stichproben die gleiche Anzahl an Probanden haben.

Sind also unsere Daten nicht intervallskaliert oder sind unsere intervallskalierten Daten nicht normalverteilt, so können wir keine Annahmen über eine mögliche Kennwertverteilung der Mittelwertsdifferenzen machen.

In diesem Falle greift man auf ein so genanntes verteilungsfreies Verfahren zurück. Im Falle zweier unabhängiger Stichproben ist dies der U-Test. Dieser Test setzt lediglich voraus, dass unsere Daten mindestens ordinalskaliert sind, denn in diesem Test wird nur die Rangfolge der Daten berücksichtigt. Hierzu folgendes Beispiel (RZ ist eine Abkürzung für Reaktionszeit):

RZ ohne Medikament	Rangplatz	RZ mit Medikament	Rangplatz
115	1	150	8
146	7	155	9
132	3	135	4
136	5	144	6
120	2	160	10

Summe der Rangplätze (=T₁) in 1.Gruppe: 18

Summe der Rangplätze (=T₂) in 2.Gruppe: 37

Nullhypothese: Beide Gruppen unterscheiden sich nicht in Bezug auf RZ

Alternativhypothese: RZ mit Medikament ist größer als RZ ohne Medikament (Dies

bedeutet, dass die zweite Gruppe langsamer reagiert als die erste

Gruppe).

Wir gehen folgendermaßen vor:

1) Wir bringen die Daten in eine gemeinsame Rangordnung. Siehe oben angeführte Tabelle (Hier kann das Problem entstehen, dass bei gleichen Zahlen so genannte verbundene Rangplätze ermittelt werden müssen. Für ein erstes grobes Verständnis des U-Tests lasse ich diesen Fall hier weg)

Trifft die Alternativhypothese zu, so müssten die Rangplätze der ersten Gruppe (der Kontrollgruppe) sämtlich vor der zweiten Gruppe liegen.

Die Rangplätze müssten also nach Annahme der Alternativhypothese wie folgt verteilt sein:

1.Gruppe	2.Gruppe
1	6
2	7
3	8
4	9
5	10

Gemäß der Nullhypothese müssten die Rangplätze dagegen gleichmäßig auf beide Gruppen verteilt sein, also etwa wie folgt:

1.Gruppe	2.Gruppe
1	2
3	4
5	6
7	8
9	10

Als nächstes prüfen wir nach, wie häufig ein Rangplatz in der ersten Gruppe größer ist als ein Rangplatz in der zweiten Gruppe. Trifft die Alternativhypothese zu, so müsste diese Häufigkeit gleich Null sein, da alle Rangplätze in der ersten Gruppe niedriger sein müssten als in der zweiten Gruppe. Anders ausgedrückt: Nach Annahme der Nullhypothese kann es nie vorkommen, dass ein Wert in der ersten Gruppe in der Rangreihenfolge nach einem Wert in der zweiten Gruppe kommt.

Diese Häufigkeit erhalten wir wie folgt:

Die erste Person in Gruppe2 hat den Rangplatz 8. Null Personen in Gruppe1 haben einen höheren Rangplatz. Die zweite Person der Gruppe2 hat Rangplatz 9. Null Personen der Gruppe1 haben einen höheren Rangplatz. Die dritte Person von Gruppe2 hat Rangplatz 4. 2 Personen in Gruppe1 haben einen höheren Rangplatz (7 und 5). Die vierte Person in Gruppe2 hat Rangplatz 6. 1 Person in Gruppe1 hat einen höheren Rangplatz. Damit haben wir insgesamt 2 + 1 = 3 Rangplatzüberschreitungen.

Diese Zahl 3 gilt nun als die so genannte Prüfgröße U. Die Zahl U gibt uns an, wie viele Rangplatzüberschreitungen in Gruppe1 gegenüber der Gruppe2 wir insgesamt haben. Nach Annahme der Alternativhypothese müsste die Anzahl der Rangplatzüberschreitungen gleich Null sein.

Je kleiner U ist, umso wahrscheinlicher ist die Alternativhypothese.

Das angegebene Beispiel wurde allerdings nur aus Demonstrationszwecken ausgewählt. Wir haben aus didaktischen Zielsetzungen eine künstliche Situation konstruiert, wie sie in der Praxis kaum vorkommt. Künstlich war die Situation insbesondere aus den folgenden beiden Gründen:

1) Wir haben die Anzahl der Rangplatzüberschreitungen einfach durch auszählen gewonnen.

2) Wir haben die Richtung der Alternativhypothese von vornherein festgelegt und auch die Daten so konstruiert, dass die Richtung auf den ersten Blick aus den Daten ersichtlich wird.

Tatsächlich verwendet man beim U-Test folgende Vorgehensweise:

1) Berechnung von U nach der Formel:

Die verwendete Prüfgröße ist das kleinere von U bzw. U'.

Auf unser konkretes Beispiel angewandt:

U = 25 + 15 - 18 = 22

Da U' < U ist, ist U' die gesuchte Prüfgröße. (Das Ergebnis ist gleich dem vorherigen Auszählen).

2) Festlegung der Richtung der Alternativhypothese:

Wir dividieren die Rangsummen T₁ und T₂ jeweils durch die Anzahl und erhalten so die jeweiligen mittleren Rangplätze der Gruppen 1 und 2, also:

18/5 = 3.6

37/5 = 7.4

Da der mittlere Rangplatz der 2.Gruppe größer ist als jener der ersten Gruppe legt sich die Vermutung nahe, dass die Rangplätze der zweiten Gruppe hinter den Rangplätzen der ersten Gruppe liegen.

3) Vergleich des errechneten U = 3 bei N1 = 5 und N2 = 5 mit dem kritischen U-Wert. Regel: Ist U_errechnet ≤ U_kritisch, so entscheiden wir uns für die Alternativhypothese (je kleiner das U, desto wahrscheinlicher die Alternativhypothese).

Bei einseitiger Hypothesenprüfung ist U_kritisch = 4.

Wir haben in diesem Falle ein signifikantes Ergebnis (weil 3 ≤ 4)!

Kritische Werte von U für den Test von Mann-Whitney (auch U-Test) für den einseitigen Test: 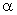=0,05

n1	n2
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
l	-
2	-	-
3	-	-	0
4	-	-	0	1
5	-	0	1	2	4
6	-	0	2	3	5	7
7	-	0	2	4	6	8	11
8	-	1	3	5	8	10	13	15
9	-	1	4	6	9	12	15	18	21
10	-	1	4	7	11	14	17	20	24	27
11	-	1	5	8	12	16	19	23	27	31	34
12	-	2	5	9	13	17	21	26	30	34	38	42
13	-	2	6	10	15	19	24	28	33	37	42	47	51
14	-	3	7	11	16	21	26	31	36	41	46	51	56	61
15	-	3	7	12	18	23	28	33	39	44	50	55	61	66	72
16	-	3	8	14	19	25	30	36	42	48	54	60	65	71	77	83
17	-	3	9	15	20	26	33	39	45	51	57	64	70	77	83	89	96
18	-	4	9	16	22	28	35	41	48	55	61	68	75	82	88	95	102	109
19	0	4	10	17	23	30	37	44	51	58	65	72	80	87	94	101	109	116	123
20	0	4	11	18	25	32	39	47	54	62	69	77	84	92	100	107	115	123	130	138
21	0	5	11	19	26	34	41	49	57	65	73	81	89	97	105	113	121	130	138	146
22	0	5	12	20	28	36	44	52	60	68	77	85	94	102	111	119	128	136	145	154
23	0	5	13	21	29	37	46	54	63	72	81	90	98	107	116	125	134	143	152	161
24	0	6	13	22	30	39	48	57	66	75	85	94	103	113	122	131	141	150	160	169
25	0	6	14	23	32	41	50	60	69	79	89	98	108	118	128	137	147	157	167	177
26	0	6	15	24	33	43	53	62	72	82	92	103	113	123	133	143	154	164	174	185
27	0	7	15	25	35	45	55	65	75	86	96	107	117	128	139	149	160	171	182	192
28	0	7	16	26	36	46	57	68	78	89	100	111	122	133	144	156	167	178	189	200
29	0	7	17	27	38	48	59	70	82	93	104	116	127	138	150	162	173	185	196	208
30	0	7	17	28	39	50	61	73	85	96	108	120	132	144	156	168	180	192	204	216
31	0	8	18	29	40	52	64	76	88	100	112	124	136	149	161	174	186	199	211	224
32	0	8	19	30	42	54	66	78	91	103	116	128	141	154	167	180	193	206	218	231
33	0	8	19	31	43	56	68	81	94	107	120	133	146	159	172	186	199	212	226	239
34	0	9	20	32	45	57	70	84	97	110	124	137	151	164	178	192	206	219	233	247
35	0	9	21	33	46	59	73	86	100	114	128	141	156	170	184	198	212	226	241	255
36	0	9	21	34	48	61	75	89	103	117	131	146	160	175	189	204	219	233	248	263
37	0	10	22	35	49	63	77	91	106	121	135	150	165	180	195	210	225	240	255	271
38	0	10	23	36	50	65	79	94	109	124	139	154	170	185	201	216	232	247	263	278
39	1	10	23	38	52	67	82	97	112	128	143	159	175	190	206	222	238	254	270	286
40	1	11	24	39	53	68	84	99	115	131	147	163	179	196	212	228	245	261	278	294

Kritische Werte von U für den Test von Mann-Whitney (auch U-Test) für den zweiseitigen Test: 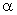=0,05

n1	n2
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	-
2	-
3	-	-	-
4	-	-	-	0
5	-	-	0	1	2
6	-	-	1	2	3	5
7	-	-	1	3	5	6	8
8	-	0	2	4	6	8	10	13
9	-	0	2	4	7	10	12	15	17
10	-	0	3	5	8	11	14	17	20	23
11	-	0	3	6	9	13	16	19	23	26	30
12	-	1	4	7	11	14	18	22	26	29	33	37
13	-	1	4	8	12	16	20	24	28	33	37	41	45
14	-	1	5	9	13	17	22	26	31	36	40	45	50	55
15	-	1	5	10	14	19	24	29	34	39	44	49	54	59	64
16	-	1	6	11	15	21	26	31	37	42	47	53	59	64	70	75
17	-	2	6	11	17	22	28	34	39	45	51	57	63	69	75	81	87
18	-	2	7	12	18	24	30	36	42	48	55	61	67	74	80	86	93	99
19	-	2	7	13	19	25	32	38	45	52	58	65	72	78	85	92	99	106	113
20	-	2	8	14	20	27	34	41	48	55	62	69	76	83	90	98	105	112	119	127
21	-	3	8	15	22	29	36	43	50	58	65	73	80	88	96	103	111	119	126	134
22	-	3	9	16	23	30	38	45	53	61	69	77	85	93	101	109	117	125	133	141
23	-	3	9	17	24	32	40	48	56	64	73	81	89	98	106	115	123	132	140	149
24	-	3	10	17	25	33	42	50	59	67	76	85	94	102	111	120	129	138	147	156
25	-	3	10	18	27	35	44	53	62	71	80	89	98	107	117	126	135	145	154	163
26	-	4	11	19	28	37	46	55	64	74	83	93	102	112	122	132	141	151	161	171
27	-	4	11	20	29	38	48	57	67	77	87	97	107	117	127	137	147	158	168	178
28	-	4	12	21	30	40	50	60	70	80	90	101	111	122	132	143	154	164	175	186
29	-	4	13	22	32	42	52	62	73	83	94	105	116	127	138	149	160	171	182	193
30	-	5	13	23	33	43	54	65	76	87	98	109	120	131	143	154	166	177	189	200
31	-	5	14	24	34	45	56	67	78	90	101	113	125	136	148	160	172	184	196	208
32	-	5	14	24	35	46	58	69	81	93	105	117	129	141	153	166	178	190	203	215
33	-	5	15	25	37	48	60	72	84	96	108	121	133	146	159	171	184	197	210	222
34	-	5	15	26	38	50	62	74	87	99	112	125	138	151	164	177	190	203	217	230
35	-	6	16	27	39	51	64	77	89	103	116	129	142	156	169	183	196	210	224	237
36	-	6	16	28	40	53	66	79	92	106	119	133	147	161	174	188	202	216	231	245
37	-	6	17	29	41	55	68	81	95	109	123	137	151	165	180	194	209	223	238	252
38	-	6	17	30	43	56	70	84	98	112	127	141	156	170	185	200	215	230	245	259
39	0	7	18	31	44	58	72	86	101	115	130	145	160	175	190	206	221	236	252	267
40	0	7	18	31	45	59	74	89	103	119	134	149	165	180	196	211	227	243	258	274