T-Test für unabhängige Stichproben
Wir gehen von folgendem Beispiel aus: Wir erheben zwei Zufallstichproben, wobei nur die Probanden der einen Stichprobe einer speziellen experimentellen Behandlung (etwa die Verabreichung eines Medikaments) unterzogen werden. Die andere Stichprobe fungiert als Kontrollgruppe für Vergleichszwecke.
In der Kontrollgruppe erhalten die Probanden also in unserem Beispiel kein Medikament. Die Frage ist nun: Ist der Unterschied zwischen dem Mittelwert in der Kontrollgruppe vom Mittelwert in der behandelten Gruppe statistisch auffällig?
Nehmen wir an, wir hätten folgendes Ergebnis bei unseren beiden Stichproben erhalten:
Um diesen Unterschied nun inferenzstatistisch zu bewerten, verwenden wir die gleiche Logik, wie sie bereits bisher zur Anwendung kam. Wir formulieren zunächst eine Nullhypothese und eine Alternativhypothese.
Die Nullhypothese lautet: Die Mittelwerte beider Stichproben entstammen zwei Populationen mit identischem Mittelwert, daher gilt:
µ1= µ2 bzw. µ1 - µ2 = 0
Die Alternativhypothese dagegen lautet:
µ1 ≠ µ2
Wir fragen: Wie
wahrscheinlich ist es, unter Geltung der Nullhypothese eine derartige
Abweichung zu bekommen? Um diese Wahrscheinlichkeit nun zu berechnen,
benötigen wir wiederum eine Kennwertverteilung. Unsere
Kennwertverteilung ist in diesem Falle die Verteilung der
Mittelwertsdifferenzen (dies ist die Verteilung der 
). Wie man zu dieser Verteilung kommt, kann man sich an
dem folgenden künstlichen Szenario vergegenwärtigen: Wir ziehen aus
den beiden Populationen immer wieder paarweise unabhängige Stichproben. Für
jedes dieser Stichprobenpaare wird die Differenz berechnet. Die Verteilung dieser Differenzen
ist unsere gesuchte Kennwertverteilung.
Eine weitere Frage ist, welche durchschnittliche Differenz wir erwarten können, wenn beide Stichproben aus Populationen mit identischem Mittelwert entstammen. Diese erwartete Differenz entspricht der in der Nullhypothese beschriebenen Differenz. Diese ist in unserem Beispiel = 0.
Konkret stellt sich nun die Frage: Wie wahrscheinlich ist es, aus einer Kennwertverteilung von Mittelwertsdifferenzen mit einem Mittelwert von 0 eine Differenz von 5 ms zu erhalten - wie in unserem Beispiel.
Dazu müssen wir, wie bereits gesagt, die Kennwertverteilung kennen. Da wir hier von zwei Stichproben ausgehen, sind uns die Varianzen in den beiden Populationen nicht bekannt.
Die Form dieser Kennwertverteilung hängt vom Stichprobenumfang ab. Wir müssen zwei Fälle unterscheiden:
1) Beträgt der Stichprobenumfang je Stichprobe ca. 30 Probanden (Faustregel!!), so können wir davon ausgehen, dass die Kennverteilung normalverteilt ist.
2) Bei kleineren Stichprobenumfängen ist die Verteilung der Mittelwertsdifferenzen t-verteilt. Voraussetzung zur genauen Berechnung der t-Verteilung ist aber, dass beide Populationen, aus denen die Daten unserer beiden Stichproben stammen, normalverteilt sind.
1)
Vorgehensweise bei großen Stichprobenumfängen
a) Wir berechnen die Differenz der Mittelwerte, also 110 - 105
b) Da die Kennwertverteilung bei großen Stichprobenumfängen normalverteilt ist, verwenden wir die z-Transformation
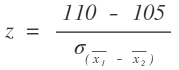
c) Die Standardabweichung der Mittelwertsdifferenzen - auch Standardfehler der Mittelwertsdifferenz genannt - berechnen wir nach der Formel:
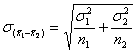
d) Da die Varianzen der beiden Populationen nicht bekannt sind, müssen sie aus den beiden Stichprobenvarianzen geschätzt werden.
Der Stichprobenumfang der ersten Stichprobe sei: n1 = 125; der zweiten Stichprobe n2 = 150.
Die geschätzten Populationsvarianzen erhalten
wir, indem wir die Summe der Abweichungsquadrate in den beiden
Stichproben (= Summe der 
) jeweils durch n - 1 dividieren.
Nehmen wir an, wir hätten folgende Schätzungen der Populationsvarianzen erhalten:
σ12 = 12,5 ; σ22 = 10.
Den Standardfehler der Mittelwertsdifferenzen berechnen wir nun nach der Formel:
e) Wir erhalten den folgenden z-Wert:
Ein z von 12,19 ist deutlich größer als ein zkritisch von 1,96 (bei zweiseitiger Hypothesenprüfung) und damit ein hoch signifikantes Ergebnis.
2)
Vorgehensweise bei kleineren Stichprobenumfängen
a) Wir berechnen die Differenz der Stichprobenmittelwerte, also 110 - 105.
b) Bei kleineren Stichprobenumfängen ist die Kennwertverteilung (= die Verteilung der Mittelwertsdifferenzen) unter der Voraussetzung, dass die Daten in der Population normalverteilt sind, t-verteilt. Wir verwenden daher die t-Transformation.
c) Bei kleineren Stichprobenumfängen ist an die Berechnung der Standardabweichung der Mittelwertsdifferenzen - auch Standardfehler der Mittelwertsdifferenz genannt - eine weitere wesentliche Voraussetzung geknüpft: Um einen t-Test für unabhängige Stichproben berechnen zu können, müssen die Varianzen in den beiden Populationen, aus denen die Stichproben stammen, gleich sein.
Wegen dieser unterstellten Gleichheit der Varianzen wird der geschätzte Standardfehler der Mittelwertsdifferenzen etwas anders als im ersten Falle berechnet. Aus der Gleichheit der Varianzen folgt nämlich:
σ12 = σ22
Da laut Voraussetzung die Varianzen der beiden Stichproben zwei Schätzungen der gleichen Populationsvarianz darstellen, berechnen eine gemeinsame Schätzung der Varianz nach der Formel:
(Man beachte: σ12 und σ22 sind die jeweiligen Schätzungen der Populationsvarianz, basierend auf den Streuungen in den beiden Stichproben!)
Für den Standardfehler der Mittelwertsdifferenzen ergibt sich daraus:
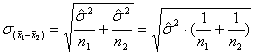
d) Der Stichprobenumfang der ersten Stichprobe sei: N1 = 5; der zweiten Stichprobe N2 = 6.
Die geschätzten Populationsvarianzen erhalten
wir auf die gleiche Weise wie im Fall 1: Indem wir nämlich die Summe der
Abweichungsquadrate in den beiden Stichproben (Summe der ) jeweils durch n - 1 dividieren.
Gehen wir wiederum von den gleichen Schätzungen der beiden Populationsvarianzen aus:
σ12 = 12,5 ; σ22 = 10.
Die gemeinsame Schätzung der Populationsvarianz ergibt dann:
= 11.11
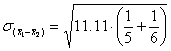= 2.018
e) Wir erhalten den folgenden t-Wert:
= 5 / 2.018 = 2.47
Dieser t-Wert ist mit n1 - 1 + n2 - 1 = n1 + n2 - 2 Freiheitsgraden t-verteilt.
Wir erhalten auf einem 5% Signifikanzniveau bei 5+6 - 2 = 9 Freiheitsgraden im Falle einer zweiseitigen Hypothesenprüfung ein tkritisch von 2,262
Ein t von 2,47 ist größer als ein tkritisch von 2,262 (bei zweiseitiger Hypothesenprüfung) und damit können wir die H0 verwerfen und erhalten ein signifikantes Ergebnis.