Rangkorrelation

Rangkorrelation

Die Themen Korrelation und Regression haben wir in den vorangehenden Kapiteln nur unter dem Gesichtspunkt und der Voraussetzung betrachtet, dass die Daten intervallskaliert sind. Wie wir gesehen haben, kamen bei der Berechung des Korrelationskoeffizienten und auch bei der Regression die statistischen Kennwerte Mittelwert und Varianz zur Anwendung. Nun ist es indes, wie bereits wissen, unzulässig, Mittelwerte und Varianzen für ordinalskalierte Daten zu berechnen. Im Folgenden gehen wir der Frage nach, welches Zusammenhangsmaß wir bei ordinalskalierten Daten verwenden können. Dafür gibt es spezielle Verfahren, so genannte Rangkorrelationen (wegen ihrer Anwendung auf rangskalierte Daten).

Wir können bei der Berechnung von Rangkorrelationen zwei Betrachtungsebenen unterscheiden: Das reine Rechenverfahren, also der Algorithmus als solches und die dahinter stehende Theorie.

Es gibt verschiedene Verfahren zur Berechnung der Rangkorrelation. Exemplarisch wird hier der Rangkorrelationskoeffizient nach Spearman vorgestellt. Dieser ist der älteste, wenngleich aber nicht unbedingt schärfste Test zur Berechnung der Rangkorrelation. Aus historischen Gründen hat er sich allerdings am längsten gehalten. Wichtiger als das reine Rechenverfahren ist die dahinter stehende generelle Theorie. Verstehen Sie den theoretischen Ansatz, so können Sie unschwer mit Hilfe eines Computerprogramms auch andere Verfahren zur Berechnung der Rangkorrelation heranziehen. Zur Veranschaulichung der Grundidee, die hinter dem Konzept der Rangkorrelation steckt, ist jedenfalls der Rangkorrelationskoeffizient nach Spearman geeignet.

Beginnen wir mit dem Rechenverfahren und betrachten dazu ein aus didaktischen Gründen sehr vereinfachtes Beispiel:

Gehen wir wieder von zwei Reaktionszeiten gemessen in ms aus, wobei in diesem Falle nur die ordinale Information der Daten für die Korrelation berücksichtigt werden soll. Das bedeutet: Wir ordnen die Reaktionszeiten zwar der Größe nach, die Abstände zwischen den einzelnen Messwerten sind aber nicht definiert. Beispiel:

x	y
40	44
18	14
24	26
19	25

Zuerst bringen wir die Reaktionszeiten vor und nach Verabreichung des Medikaments jeweils in eine Rangordnung, also:

x	y	d_i	d_i²
4	4	0	0
1	1	0	0
3	3	0	0
2	2	0	0

d_iist die Differenz zwischen dem ersten und dem zweiten Rangplatz, was in diesem Beispiel immer 0 beträgt, d_i²ist die quadrierte Differenz. Den Spearman-Rangkorrelationskoeffizienten berechnen wir nun nach der Formel:

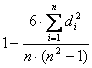
n ist in diesem Falle 4.

r_s = 1!

Betrachten wir nun noch den zweiten, umgekehrten Fall:

x	y
40	14
18	44
24	25
19	26

Daraus ergibt sich folgende Rangordnung:

x	y	d_i	d_i²
4	1	3	9
1	4	-3	9
3	2	1	1
2	3	-1	1

Daraus ergibt sich ein r_s von:

Wir sehen aus den beiden trivialen Beispielen, dass der Rangkorrelationskoeffizient r_s zwischen +1 und -1 angesiedelt ist.

Tatsächlich wird r_s nicht genau -1 bzw. +1 sein - wie in den beiden idealisierten Beispielen - sondern irgendwo dazwischen liegen. Dazu ein konkretes Beispiel:

Nehmen wir an 10 Personen wurden von zwei verschiedenen Schiedsrichtern hinsichtlich ihrer Beherrschung verschiedener Tanzdisziplinen jeweils in eine Rangordnung gebracht. Die zwei verschiedenen Bewertungen der beiden Schiedsrichter sind unsere beiden Variablen und die Ranglätze der einzelnen Probanden sind die Ausprägung der Variablen.

Die Frage, die gestellt werden kann, ist nun die folgende: Inwiefern stimmt die Rangordnung der Variable x mit der Rangordnung der Variable y überein? Anders formuliert, mehr auf unser praktisches Beispiel bezogen ausgedrückt bedeutet dies: Inwiefern stimmen die beiden Schiedsrichter in ihrer Beurteilung überein? Ein Maß, um diese Übereinstimmung überprüfen zu können, ist der Rangkorrelationskoeffizient nach Spearman.

In einem konkreten Falle würden uns die beiden Schiedsrichter für die 10 Probanden folgende Bewertungen abgeben:

Proband	Schiedsrichter 1	Schiedsrichter 2	d_i	d_i²
1	6	4	2	4
2	4	1	3	9
3	3	6	-3	9
4	1	7	-6	36
5	2	5	-3	9
6	7	8	-1	1
7	9	10	-1	1
8	8	9	-1	1
9	10	3	7	49
10	5	2	3	9

Die Summe der d_i² beträgt in diesem Falle 128; n (die Anzahl der Probanden) ist 10.

Wir können daher r_s ausrechnen:

Ein Rangkorrelationskoeffizient von 0.224 ist nicht sehr hoch, woraus wir darauf schließen können, dass die Übereinstimmung bzw. der Zusammenhang zwischen den Urteilen der beiden Schiedsrichter nicht sehr groß ist.

Verbundene Rangplätze

Bei gleichen Skalenwerten werden so genannte verbundene Rangplätze verwendet: Haben mehrere Probanden den gleichen Skalenwert, so erhalten sie den Durchschnitt der normalerweise an sie zu vergebenden Rangplätze (Beispiel: 2 Probanden teilen sich den gleichen Platz, da sie die gleichen Werte haben; jeder der beiden Probanden bekommt so den Rangplatz (2+3)/2= 2,5!

Beispiel:

Schulnote in Mathematik (x)	Schulnote in Informatik (y)
2	3
4	5
2	3
3	3
3	1
2	2
1	2
3	3
4	4
3	3

Daraus ergibt sich folgende Rangordnung:

x	y	d_i²
3	6	9
9.5	10	0.25
3	6	9
6.5	6	0.25
6.5	1	30.25
3	2.5	0.25
1	2.5	2.25
6.5	6	0.25
9.5	9	0.25
6.5	6	0.25

Da sich die Formel zur Berechnung des Rangkorrelationskoeffizienten ändert, wenn die Gesamtanzahl der verbundenen Rangplätze mehr als 20% aller Rangplätze ausmacht, gehe ich hier nicht weiter darauf ein.

Denn in der Praxis werden Sie eine Rangkorrelation mit EDV-Methoden berechnen. Die zentrale Frage hingegen ist, wie ein Rangkorrelationskoeffizient zu interpretieren ist.

Beachten Sie zunächst, dass die Abstände zwischen den Reaktionszeiten bei ordinalskalierten Daten keine Rolle spielt. Betrachten wir zur Veranschaulichung nochmals das allererste Beispiel:

V1 V2

40 44 (5435)

18 14

24 26

19 25

Was hätte sich geändert, wenn wir statt 44 bei der zweiten Messung der ersten Person die Zahl 5435 ms feststellen müssten?

Auch in diesem Falle erhielten wir die gleiche Rangordnung, d.h.:

V1 V2 d_i d_i²

4 4 0 0

1 1 0 0

3 3 0 0

2 2 0 0

Wir bekämen also den gleichen Wert für r_s, wenn wir für 44 die Zahl 5435 substituieren!

Vor dem Hintergrund dieser Überlegungen kommen wir nun zu der hinter der Rangkorrelation stehenden Theorie. Was bedeutet ein hoher (absoluter) Wert von r_s?

Er bedeutet: Einer Zunahme in der x-Richtung entspricht eine Zunahme (im Falle einer negativen Korrelation: eine Abnahme) in der y-Richtung.

Kurz und prägnant ausgedrückt bedeutet dies: ∆x -> ∆y

Wir können allerdings nicht sagen, um wie viel Maßeinheiten sich die y-Werte aufgrund der x-Werte erhöhen werden.

Das bedeutet mathematisch: Zwischen x-Werten und y-Werten besteht eine monotone Beziehung. Eine Rangkorrelation verwendet keine metrischen Maßeinheiten. Tragen wir die Zahlenpaare in einem Koordinatensystem ein, so befinden sich die dargestellten Punkte in keinem metrisch beschreibbaren euklidischen Raum.

Aus diesem Grunde lässt sich im Falle einer Rangkorrelation, also bei ordinalskalierten Daten auch keine Regressionsgerade berechnen. Weder die Berechnung des Anstiegs noch der Abschnitt auf der y-Achse ergäbe einen Sinn. Um es nochmals zu betonen: Bei Rangkorrelationen gibt es keine Maßeinheiten, kein "wie viel mal größer" bzw. "wie viel mal kleiner" und somit keine Regressionsgerade.

Um die Bedeutung dieses Umstands besser einschätzen zu können, knüpfen wir an eine Überlegung aus der Messtheorie an: Was sind überhaupt Skalen? Es sind Zahlzeichen, die bestimmte Eigenschaften der sozialwissenschaftlichen Realität, die sie abbilden, reflektieren. Wir können uns dies auch an dem folgenden ganz allgemeinen Beispiel verdeutlichen: An einem Flugsimulator kann das Fliegen erlernt werden. Der Flugsimulator selber ist kein konkretes Flugzeug und die Steuerbewegungen, die wir mit einem virtuellen Steuerknüppel durchführen, führen auch nicht zu einer tatsächlichen Steuerung eines Flugzeuges.

Was ist also der Flugsimulator? Er ist ein Modell eines tatsächlichen Fluges. Dieses Modell reflektiert nun aber Eigenschaften, die auch bei der tatsächlichen Steuerung eines Flugzeuges auftreten. Würde das Modell nicht derartige Eigenschaften reflektieren, so könnte man mit einem Flugsimulator überhaupt nicht Fliegen lernen. Und je besser der Flugsimulator einen Echtflug modelliert, umso brauchbarer ist er. Problematisch wird es, wenn in unserem Flugsimulator Eigenschaften auftreten, die nicht der tatsächlichen Situation bei der Steuerung eines Flugzeugs entsprechen. Ein derartiger Unterschied zwischen dem Modell und der simulierten Realität kann im Ernstfall tödliche Konsequenzen nach sich ziehen.

Nun zurück zu unseren Zahlenzeichen: Auch sie sind nichts anderes als ein Modell der dahinter stehenden Realität, die sie abbilden. Die Frage ist nun, ob unser Modell am Ende Eigenschaften hat, die sich nicht in der sozialwissenschaftlichen Realität wieder finden.

Rein intuitiv sind wir es gewöhnt, unseren Zahlen gewisse Eigenschaften zuzusprechen: Wir können sie addieren, multiplizieren, dividieren usw.

Unsere Zahlen als solche bilden - intuitiv gesprochen - einen euklidischen Raum. Nur in einem euklidischen Raum entsprechen Zahlen messbare Punkte in einem Koordinatensystem und nur dort sind die Abstände zwischen diesen Punkten auch genau definiert. Und nur in einem solchen Falle ergibt es überhaupt einen Sinn, zwischen den Punkten eine Gerade durchzuziehen.

Denken wir nun aber an unseren lebensweltlichen Alltag, wie wir ihn in unserer Alltagssprache beschreiben. Nähe- und Ferne-Beziehungen (ein Mensch steht uns nahe oder fern) in diesem Alltag sind nicht unbedingt metrisch. Wir können beispielsweise sagen, dieser Mensch ist uns sympathischer als ein anderer, aber nicht, um wie viel Maßeinheiten.

Versuchen wir nun, für Menschen eine Skala der Sympathie zu verwenden, so müssen wir dem Umstand Rechnung tragen, dass die dabei verwendeten Zahlzeichen nicht metrisch sind. Wir dürfen also beim Umgang mit diesen Zahlen keine Eigenschaften von Zahlen verwenden, die Intervallskala voraussetzen. Stattdessen dürfen wir nur solche Eigenschaften verwenden, die auch die tatsächlich dahinterstehende sozialwissenschaftliche Realität reflektieren. Wir wissen nur, dass eine Zunahme der Sympathie auch eine Zunahme der zugeordneten Zahl bewirkt, wir wissen aber nicht um wie viel Maßeinheiten die Zahl größer wird, wenn die Sympathie steigt.

Betrachten wir nun zwei ordinalskalierte Variablen, wie wir sie zur Berechung einer Rangkorrelation benötigen: Wir wollen herausfinden, ob zwischen Sympathiewerten und der Zufriedenheit eines Menschen ein Zusammenhang besteht. Auch die Zufriedenheit eines Menschen verschlüsseln wir in Zahlzeichen. Eine größere Zahl bedeutet dabei ein mehr an Zufriedenheit.

Zwischen den Zahlzeichen für Zufriedenheit und der tatsächlichen Zufriedenheit besteht eine monotone Beziehung, ebenso zwischen den Zahlzeichen für Sympathie und der tatsächlichen Sympathie.

Man kann sich das tabellarisch wie folgt überlegen:

Zufriedenheit	Sympathie	monotone Beziehung
Skala der Zufriedenheit	Skala der Sympathie	monotone Beziehung
monotone Beziehung	monotone Beziehung

Besteht zwischen "Zufriedenheit" und "Sympathie" eine monotone Beziehung, so überträgt sich dieser Umstand auch auf die Beziehung zwischen den Skalenwerten von Zufriedenheit und Sympathie (da zwischen "Zufriedenheit" und Skala der Zufriedenheit bzw. "Sympathie" und Skala der Sympathie ebenfalls eine monotone Beziehung besteht)

Man beachte: Man kann Rangkorrelationen auch bei Intervallskalen verwenden. Das tut man dann, wenn andere Voraussetzungen zur Berechnung des Produktmomentkorrelationskoeffizienten nicht erfüllt sind (bivariate Normalverteilung; zu kleiner Stichprobenumfang).

Inferenzstatistische Absicherung

Auch für den Rangkorrelationskoeffizienten nach Spearman ist, ähnlich wie beim Korrelationskoeffizienten nach Pearson Bravais, eine inferenzstatistische Absicherung notwendig. Auch hier soll abgeschätzt werden, inwiefern das errechnete rs signifikant von einem ρ=0 abweicht. Für Fälle bis zu 30 Probanden ist hierfür die folgende Tabelle geeignet:

Anzahl der Probanden	*p=0,05*	*p=0,01*
5	1
6	0,886	1
7	0,786	0,929
8	0,738	0,881
9	0,683	0,833
10	0,648	0,794
12	0,591	0,777
14	0,544	0,715
16	0,506	0,665
18	0,475	0,625
20	0,45	0,591
22	0,428	0,562
24	0,409	0,537
26	0,392	0,515
28	0,377	0,496
30	0,364	0,478

(Tabelle nach Dr. Graham Hole, http://www.sussex.ac.uk/Users/grahamh/RM1web/teaching08-RS.html)

Bei unserem Beispiel mit den beiden Schiedsrichtern errechneten wir ein rs von 0,224. Laut Tabelle beträgt der kritische rs-Wert für 10 Probanden auf dem 5%-Signifikanzniveau 0,648. Unser errechnetes rs liegt damit deutlich unter dem kritischen rs, sodass die Nullhypothese nicht verworfen werden kann.

Bei mehr als 30 Probanden kann man den rs-Wert in einen t-Wert nach der folgenden Formel umwandeln

Achtung: Im Gegensatz zur obigen Tabelle muss zur Bestimmung des kritischen t-Wertes die Anzahl der Freiheitsgrade (= Anzahl der Probanden – 2) herangezogen werden.