Punktbiseriale Korrelation

Es wird der Zusammenhang zwischen einer natürlich  dichotomen  Variablen und  einer  intervallskalierten Variablen berechnet.  Auch für diesen Korrelationskoeffizienten  gilt:  Kodiert man die Ausprägungen des dichotomen Merkmals mit den Werten 0  und 1, so ist der punktbiseriale  Korrelationskoeffizient  mit dem Produkt-Moment-Korrelationskoeffizienten identisch.

Wozu benötigt man die punktbiseriale Korrelation? Eine  wesentliche Anwendung liegt in der Testtheorie. Stellen Sie sich vor, Sie hätten einen Schulleistungstest erarbeitet, indem eine Reihe von Teilaufgaben zu lösen ist. Sie bewerten die Leistung einfach an  der Summe  der gelösten Aufgaben. Jeder Proband bekommt die  gleichen Aufgaben gestellt - beispielsweise 20 Aufgaben. Für jede  gelöste Aufgabe  erhält  er einen Punkt. Die beste Leistung  pro  Proband sind somit 20 Punkte.

Angenommen, Sie wollen nun wissen, wie gut eine einzelne  Aufgabe die Gesamtleistung repräsentiert. Eine einzelne Aufgabe kann  nur gelöst  sein oder nicht - 0 oder 1. Die Frage ist nun,  inwiefern zwischen  der  Lösung dieser Aufgabe und der  Gesamtleistung  ein Zusammenhang besteht. Ein guter Zusammenhang würde sich vorerst - rein intuitiv gesprochen - dann ergeben, wenn Probanden, die die  Aufgabe nicht gelöst haben, auch eine  schlechte  Gesamtleistung  aufweisen,  und wenn umgekehrt Probanden,  die  die  Aufgabe gelöst haben, auch in der Gesamtleistung gut abschneiden.

Das  bedeutet:  Wir  fragen nach dem  Zusammenhang  zwischen  der Lösung einer einzelnen Aufgabe, einer natürlich dichotomen Variable also, und der Gesamtleistung, die intervallskaliert ist.

Dafür  eignet sich nun der punktbiseriale  Korrelationskoeffizient.  Er wird auch als  Trennschärfekoeffizient  bezeichnet.  Er gibt nämlich an, wie gut eine einzelne  Aufgabe  zu trennen  vermag zwischen Probanden mit einer  niederen  Gesamtleistung und solchen mit einer höheren Gesamtleistung. Diese Trennung wird umso besser sein, je höher die einzelne Aufgabe und die Gesamtleistung miteinander korrelieren.

Wie gehen wir vor?

Gehen  wir  zunächst  von der Erfassung  der  Rohdaten  aus.  Wir schreiben die beiden Variablen - die natürlich dichotome und  die intervallskalierte - nebeneinander je in eine Spalte. Beispiel:

 

 

 

x                           y

0                           4

0                           6

1                           6

0                           5

1                           12

0                           11

1                           11

1                           13

1                           16

1                           18

Die Variable x ist die natürlich dichotome Variable, die Variable y die Gesamtleistung.

Für  einen späteren Schritt benötigen wir die  Standardabweichung der  Variable  y  (diese ist in dem vorliegenden  Beispiel:  s  = 4,56).  Die Gesamtanzahl aller getesteten Personen ist 10.

In  einem nächsten Schritt unterteilen wir die Gesamtleistung  in zwei  Spalten und zwar nach dem Kriterium, ob die  einzelne  Aufgabe gelöst wurde oder nicht. Wir bezeichnen die beiden Spalten mit y₀ und y₁, also:

y₀                          y₁

4                           6

6                           12

5                           11

11                         13

                             16

                             18

y₀  enthält  4  Fälle - vier Probanden haben  die  Aufgabe  nicht gelöst  - y₁ enthält 6 Fälle - sechs Probanden haben die  Aufgabe gelöst. Wir drücken das auch so aus: n₀ = 4; n₁ = 6. Der  Mittelwert von y₀ ist 6,5; der Mittelwert von y₁ = 12,67.

Damit haben wir alle notwendigen Voraussetzungen, um r_pb  berechnen zu können.

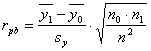
In unserem konkreten Fall ist r_pb: