Verfahren zur
Überprüfung von Zusammenhangshypothesen
Wir haben uns bisher mit Unterschiedshypothesen beschäftigt (Unterschiede von Stichproben in Bezug auf abhängige Variablen). Im Folgenden geht es um Zusammenhangshypothesen, d.h. um die Frage inwiefern Änderungen einer Variablen Rückschlüsse auf die Änderungen einer anderen Variablen zulassen.
Wozu brauchen wir das? Es geht darum,
die Werte der zweiten Variablen aufgrund der Werte der
ersten Variablen voraussagen zu können. Nennen wir
die ersten Werte x-Werte und die zweiten Werte die y-Werte. Die
Frage ist nun, inwiefern sich die y-Werte aufgrund der x-Werte
voraussagen lassen.
Unsere Voraussage wird umso zutreffender sein,
je stärker der Zusammenhang zwischen y-Werten und x-Werten
ist. Dazu benötigen wir ein Maß für den Zusammenhang.
Betrachten wir dazu das folgende Beispiel: Stellen Sie sich
vor, Sie müssten aufgrund eines Eignungstests die Begabung eines Schülers
in Mathematik feststellen. Sie würden dazu eine Punkteskala
verwenden, wobei wenige Punkte wenig Begabung und mehr
Punkte mehr Begabung bedeuten würden. Je besser nun diese
Punkte die späteren Schulnoten in Mathematik
voraussagen können, umso stärker ist der Zusammenhang
zwischen dem Eignungstest in Mathematik und den späteren Schulnoten.
Man kann zwei verschiedene Arten von
Zusammenhängen unterscheiden: funktionale Zusammenhänge, die
aufgrund einer mathematischen Funktionsgleichung exakte
Voraussagen ermöglichen und stochastische Zusammenhänge, bei
denen nur eine ungefähre Voraussage möglich ist.
Betrachten wir zum besseren Verständnis zunächst
eine einfache Funktionsgleichung:
![]()
Wir können uns den exakten mathematischen Zusammenhang an einer einfachen Tabelle verdeutlichen:
|
x |
y |
|
0 |
3 |
|
1 |
5 |
|
2 |
7 |
|
3 |
9 |
|
4 |
11 |
Überträgt man diese Zahlenpaare in ein Koordinatensystem, so erhalten wir eine Gerade mit dem Anstieg 2 (d.h.: gehen wir eine Einheit in die x-Richtung, so müssen wir zwei Einheiten in die y-Richtung gehen) und dem Abschnitt auf der y-Achse 3. (wenn x = 0 ist, dann ist y = 3)
Man erhält diese Gerade auch dann, wenn man einfach zwischen zwei Zahlenpaaren, die Punkte im Koordinatensystem darstellen, eine Verbindung herstellt.
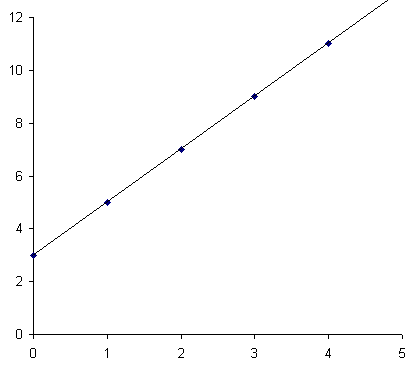
Im Falle eines derartigen exakten funktionalen Zusammenhangs
brauchen wir die y-Werte nicht extra angeben, denn sie lassen sich ja aus den
x-Werten mit Hilfe der Funktionsgleichung eindeutig berechnen. Das heißt:
Kennen wir die x-Werte und haben wir zudem die Geradengleichung, dann
können wir mit mathematischer Exaktheit die y-Werte voraussagen.
Wäre der Zusammenhang zwischen Eignungstest und Schulnoten derart
mathematisch exakt, dann könnten wir uns die späteren Prüfungen in
Mathematik ersparen.
Nun zum stochastischen Zusammenhang:
Auch beim stochastischen Zusammenhang bilden wir zunächst die Zahlenpaare in einer Tabelle. Beispiel:
|
x |
y |
|
1 |
5 |
|
2 |
8 |
|
3 |
7 |
|
4 |
10 |
|
|
|
Die Zahlenpaare sind nichts anderes als die
Werte der beiden Variablen pro Person, wobei jede Zeile
die beiden jeweiligen Werte einer Person enthält. Man kann nun auch
diese Zahlenpaare in einem Koordinatensystem eintragen. Jedem
Zahlenpaar entspricht ein Punkt in dem Koordinatensystem und jeder der Punkte
bezeichnet die beiden Messwerte für die zwei Variablen pro Person.
Im Unterschied zum funktionalen Zusammenhang
bilden die Punkte keine Gerade, sondern streuen um eine
Gerade (oder um eine andere mathematische Funktion!). Wir haben es hier mit einem
stochastischen bzw. korrelativen Zusammenhang zu tun. Die
Punkte streuen rein zufällig um die Gerade (oder um
eine andere mathematische Funktion). Je näher die
Punkte sich zur Gerade befinden, umso eher lässt sich der
stochastische Zusammenhang durch einen linearen funktionalen
Zusammenhang erklären. Die Gerade, um die die Punkte streuen,
ist also eine künstliche Idealisierung des stochastischen Zusammenhangs,
u.zw. eine Darstellung des stochastischen Zusammenhangs durch einen
linearen.
Eine derartige Streuung der Punkte bezeichnet man auch als Streuungsdiagramm oder auch als Punktediagramm.
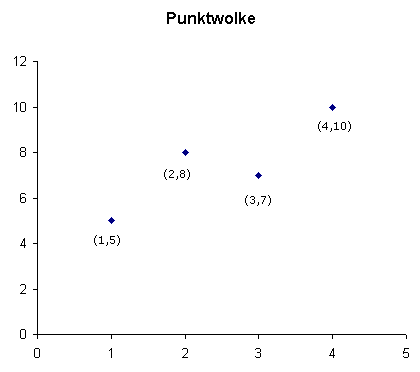
Wir brauchen nun ein Maß, das uns besagt, wie eng die
Punkte um eine idealisierte Gerade streuen. Ein derartiges
Maß ist die Kovarianz.
Die Berechnungsformel dafür ist:
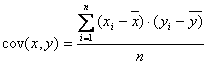
Die Kovarianz ist der Mittelwert der
Abweichungsprodukte einer bivariaten Verteilung. Sie besagt den Grad des
miteinander Variierens zweier Verteilungen.
Überlegen wir uns dies an zwei Beispielen:
1) Wir gehen zunächst davon aus, dass eine Zunahme
in der y-Richtung sich annähernd aus
einer Zunahme in der x-Richtung erklären lässt.
Höhere x-Werte ziehen höhere y-Werte nach sich. Umgekehrt
ziehen niedere x-Werte auch entsprechend niedere y-Werte nach
sich. Im idealen Falle lässt sich dies durch eine Geradengleichung
ausdrücken. Beispiel: ![]() . Wenn wir in diese Gleichung höhere
x-Werte einsetzen, so werden auch die y-Werte zunehmen. Negative x-Werte
führen zu negativen y-Werten (zu einer Verminderung der y-Werte)
und positive x-Werte zu einer Erhöhung der y-Werte (zu positiven
y-Werten).
. Wenn wir in diese Gleichung höhere
x-Werte einsetzen, so werden auch die y-Werte zunehmen. Negative x-Werte
führen zu negativen y-Werten (zu einer Verminderung der y-Werte)
und positive x-Werte zu einer Erhöhung der y-Werte (zu positiven
y-Werten).
Im Falle eines stochastischen Zusammenhanges liegen
die Zahlenpaare nicht exakt auf einer Gerade, sondern streuen zufällig
um die Gerade. Liegen die Punkte nun sehr nahe an der
Gerade, so ergibt sich der folgende Umstand:
Liegen die x-Werte über ihrem Mittelwert (d.h. haben wir
es mit überdurchschnittlich hohen x-Werten zu tun), so
liegen auch die y-Werte über ihrem Mittelwert. Wir bekommen so ein hohes
positives Produkt. (da sowohl bei x-Werten als auch bei y-Werten
eine überdurchschnittliche Abweichung vorliegt).
Liegen die x-Werte unter ihrem Mittelwert, so liegen auch
die y-Werte unter ihrem Mittelwert. Wir bekommen auch hier
ein hohes positives Produkt (zwei Zahlen mit negativen
Vorzeichen ergeben multipliziert ein positives Vorzeichen).
2) Wir gehen davon aus, dass eine Zunahme in der
y-Richtung sich durch eine Abnahme in der x-Richtung
erklären lässt. Niedere x-Werte ziehen in diesem Falle hohe
y-Werte nach sich. Umgekehrt ziehen hohe x-Werte niedere
y-Werte nach sich. Im idealen Falle bekommen wir folgende
Geradengleichung: ![]() . Setzen wir in diese Gleichung positive
x-Werte ein, so bekommen wir entsprechend negative
y-Werte. Negative x-Werte führen zu einer Erhöhung der y-Werte (zu
positiven y-Werten), umgekehrt führen positive x-Werte zu negativen
y-Werten.
. Setzen wir in diese Gleichung positive
x-Werte ein, so bekommen wir entsprechend negative
y-Werte. Negative x-Werte führen zu einer Erhöhung der y-Werte (zu
positiven y-Werten), umgekehrt führen positive x-Werte zu negativen
y-Werten.
Betrachten wir dazu folgende Tabelle:
|
X |
Y |
|
0 |
3 |
|
1 |
1 |
|
2 |
-1 |
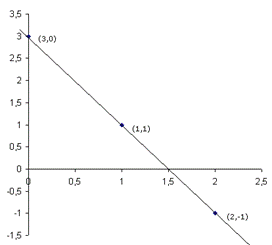
Im Falle eines stochastischen Zusammenhanges liegen
die Zahlenpaare nicht exakt auf einer Gerade, sondern streuen zufällig
um die Gerade. Liegen die Punkte nun sehr nahe an der
Gerade, so ergibt sich der folgende Umstand:
Liegen die x-Werte über ihrem Mittelwert (d.h. haben wir
es mit überdurchschnittlich hohen x-Werten zu tun), so liegen
die entsprechenden y-Werte unter ihrem Mittelwert. Wir bekommen so
ein hohes negatives Produkt.
Liegen die x-Werte unter ihrem Mittelwert, so
liegen die entsprechenden y-Werte über ihrem Mittelwert. Wir
bekommen auch hier ein hohes negatives Produkt (zwei Zahlen mit verschiedenen
Vorzeichen ergeben multipliziert ein negatives Vorzeichen).
Das Vorzeichen der Kovarianz sagt also nichts über die Stärke
des Zusammenhanges aus, sondern nur etwas über die Polung des
Zusammenhanges. Eine negative Kovarianz sagt uns, dass eine
Erhöhung der x-Werte zu einer Verminderung der y-Werte führt, eine
positive Kovarianz sagt uns umgekehrt, dass eine Erhöhung der
x-Werte auch zu einer Erhöhung der y-Werte führt.
Was sagt uns dann etwas über die Stärke des
Zusammenhanges aus? Die Höhe der absoluten Zahl - ohne Vorzeichen!
Nun ist aber die Kovarianz auch vom
verwendeten Maßstab der Variablen abhängig. Multiplizieren wir
beispielsweise die y-Werte mit dem Faktor 10, so erhalten wir auch
eine um den Faktor 10 multiplizierte Kovarianz, obwohl sich am
Zusammenhang nichts geändert hat!
Allgemein gilt: Werden die x-Werte mit dem Faktor k und die y-Werte mit dem Faktor l multipliziert, so ändert sich die Kovarianz um den Faktor k * l!
Beispiel für eine
Berechnung der Kovarianz:
|
x |
y |
|
|
|
|
3 |
3 |
-7 |
-3 |
21 |
|
7 |
5 |
-3 |
-1 |
3 |
|
11 |
7 |
1 |
1 |
1 |
|
14 |
6 |
4 |
0 |
0 |
|
15 |
9 |
5 |
3 |
15 |
![]() ;
; ![]()
Kovarianz = 40 / 5 = 8 (durchschnittliches Abweichungsprodukt)
s2x = 100 / 5 = 20; sx = 4,47
s2y = 20 / 5 = 4; sy = 2
Multiplizieren wir die y-Werte mit dem Faktor 10 (30; 50; 70; 60; 90), so erhalten wir eine Kovarianz von 80!
Dividieren wir die
Kovarianz nun durch die Standardabweichungen sx und sy,
so erhalten wir ein Zusammenhangsmaß, das gegenüber
Maßstabsveränderungen invariant ist!
Dieses Maß ist der
Korrelationskoeffizient r, auch Produkt-Moment-Korrelation
(Bravais-Pearson-Korrelation) bezeichnet:
![]()
In
unserem Beispiel: ![]()
Beispiele für Zusammenhänge:
1) hohe positive Korrelation
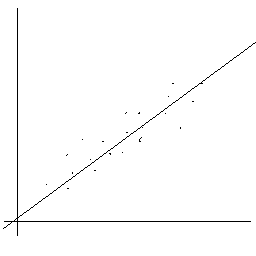
2) hohe negative Korrelation
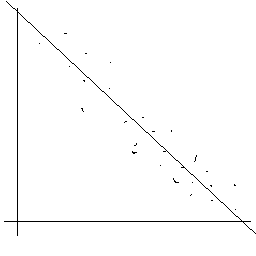
Man beachte, dass die Begriffe "positiv" bzw.
"negativ" sich nicht auf die Stärke des Zusammenhangs - diese wird
durch den Absolutbetrag von r ausgedrückt -, sondern auf die Polung
des Zusammenhangs beziehen.
3) Nichtlineare Zusammenhänge:
Beispiel: parabolischer Zusammenhang
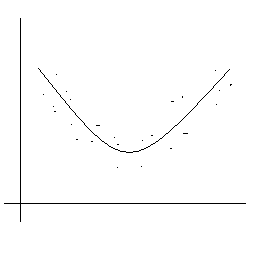
Zum besseren Verständnis der Bedeutung des
Produkt-Moment-Korrelationskoeffizienten folgende Überlegung: Was
würde geschehen, wenn wir im Falle eines solchen parabolischen Zusammenhanges
den Produkt-Moment-Korrelationskoeffizienten berechneten?
Die - vorläufige – Antwort lautet: Wir bekämen ein niedriges r!
Der Grund dafür ist der
folgende: Der Produkt-Moment-Korrelationskoeffizient berechnet den Abstand der
Zahlenpaare von einer idealen Geraden. Er ist daher ein Maß
für die Stärke des linearen Zusammenhanges. Ist
nun der Zusammenhang nicht linear (wie im Falle eines parabolischen
Zusammenhanges), so besagt das noch lange nicht, dass überhaupt
kein Zusammenhang besteht. Ein niedriges r sagt uns also nur, dass keine
Geradengleichung sinnvoll die y-Werte aus den x-Werten
voraussagen kann. Das bedeutet aber nicht automatisch, dass
es keine andere mathematische Funktion gibt, die
uns eine gute Voraussage ermöglicht.
Allgemein gilt: Wir können prinzipiell für jede beliebige
Anordnung von Punkten eine mathematische Funktion
finden, die den Zusammenhang in einer
Funktionsgleichung (keine Geradengleichung!) beschreibt.
Warum tut man das aber nicht? Warum versucht man den
Zusammenhang zwischen den Zahlenpaaren durch eine idealisierte Funktion
(durch eine Gerade oder auch eine Parabel oder
ähnliches) auszudrücken?
Dies hat einen wissenschaftstheoretischen Grund. Die
Psychologie versucht - wie jede andere Wissenschaft -
empirisch gegebene Daten auf einfache,
durchschaubare und leicht handhabbare Gesetze zurückzuführen. So ist es für uns
eben eine Information, wenn wir den Zusammenhang zwischen x-Werten und y-Werten
durch eine Geradengleichung ausdrücken können. Die
Geradengleichung ist ein intuitiv verstehbares Modell des
Zusammenhangs.
Zusammenfassend gilt für den Produkt-Moment-Korrelationskoeffizienten:
Er ist ein Maß für die Stärke der Linearität des
Zusammenhangs. Liegen alle Punkte tatsächlich auf einer Geraden, so
erhalten wir ein r von 1.
Ballen sich die Punkte um eine Punktwolke, so erhalten wir ein r
= 0.
Zu niederen x-Werten finden sich in diesem
Falle einmal hohe, zugleich aber auch niedere y-Werte (die Summe
der ![]()
Die beste Voraussage ist in diesem Falle eine
Parallele zur x-Achse.
Allgemeine Voraussetzungen zur Berechnung von r:
1) Intervallskaliertheit beider Variablen
2) die bivariate Häufigkeitsverteilung sollte normalverteilt sein (das entspricht einer Glocke im dreidimensionalen Raum)
Zur allgemeinen Bedeutung
der Korrelation:
1) kein funktionaler, deterministischer Zusammenhang
- sondern stochastischer Zusammenhang
2) keine Kausalbeziehung:
Das bedeutet:
Wenn zwischen x und y eine hohe positive Korrelation vorliegt, so
wissen wir nicht, ob
a) x y beeinflusst
b) y x beeinflusst
c) x und y von einer dritten Variable beeinflusst werden
d) x und y sich wechselseitig beeinflussen
Die Korrelation sagt lediglich, dass wir eine mathematische
Funktion gefunden haben, die annähernd den Zusammenhang von x und y
beschreibt. Warum aber dieser Zusammenhang besteht, ist
damit nicht beantwortet.
Man betrachte das folgende Beispiel:
Man kann rein statistisch einen Zusammenhang zwischen der
Fußzehengröße und der Intelligenz feststellen. Der Grund hierfür liegt einfach
daran, dass bei einer Zufallsstichprobe auch Kleinkinder miterfasst
werden. Der Zusammenhang zwischen Intelligenz und
Fußzehengröße lässt sich somit auf eine dritte Variable zurückführen: auf das
Alter!
Halten wir das Alter konstant (indem wir beispielsweise für die Korrelation zwischen Intelligenz und Fußzehengröße nut Gleichaltrige heranziehen), so verschwindet die Korrelation zwischen Fußzehengröße und Alter.
Inferenzstatistische
Absicherung
Auch bei der
inferenzstatistischen Absicherung von Zusammenhanghypothesen gibt es eine Null-
und eine Alternativhypothese.
Die
Nullhypothese lautet: es besteht kein Zusammenhang zwischen den
beiden Variabeln.
Inferenzstatistisch betrachtet bedeutet dies,
dass wir in der Gesamtpopulation ein ρ = 0 erwarten. Wir berechnen also
wie wahrscheinlich es ist, unter Geltung der Nullhypothese das berechnete r
(oder ein noch stärker von 0 abweichendes) zu bekommen. Ist diese Wahrscheinlichkeit
sehr gering (Signifikanzniveau entweder 5% oder 1%), so entscheidet man sich
für die Alternativhypothese.
Letztere besagt, dass zwischen den Variablen ein Zusammenhang besteht.
Um die
Überschreitungswahrscheinlichkeit zu berechnen, wandeln wir den r-Wert in einen
t-Wert um:
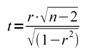
Dieser t-Wert
wird nun mit dem kritischen t-Wert der t-Tabelle mit n-2
Freiheitsgraden verglichen – ist t >= tkritisch so entscheiden
wir uns für die Alternativhypothese.
Das bedeutet in
unserem Beispiel

![]()
Da terrechnet
≥ tkritisch entscheiden wir uns für die H1.
2. Regression
Bis jetzt haben wir lediglich besprochen, wie man die
Linearität des Zusammenhangs zweier Variablen mit Hilfe des Produkt-Moment-Korrelationskoeffizienten
berechnen kann. Das Maß r sagt uns, wie sehr die stochastisch (zufällig)
verteilten Punkte um eine idealisierte Gerade streuen. Die
Frage ist nun, ob wir diese Gerade unter Zuhilfenahme des Maßes r
rechnerisch genau ermitteln können. Die Frage ist also, um welche Gerade
es sich denn eigentlich handelt.
Allgemein gilt: Jede Gerade ist mathematisch durch
die Geradengleichung festgelegt. Die Geradengleichung kennen wir bereits:
![]()
b ist der
Anstieg der Geraden, a ist der Abschnitt auf der y-Achse (die
Stelle, an der die Gerade die y-Achse schneidet, bzw. an der x = 0 ist).
Wollen wir also die idealisierte Gerade für eine bestimmte
Punktwolke ermitteln, so benötigen wir deren Koeffizienten a und b.
Nun hat die idealisierte Gerade
folgende Eigenschaft: Jedem beobachteten y-Wert (yi)
entspricht ein geschätzter y-Wert (y*i) auf
der Gerade.
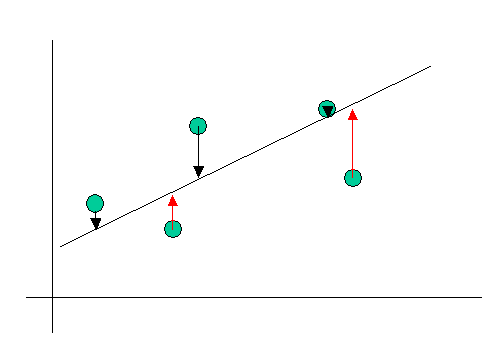
Die geschätzten und die beobachteten y-Werte weichen
voneinander ab, da die Gerade ja nur eine Schätzung des Zusammenhangs
ist. Da wir daran interessiert sind, die y-Werte aus den x-Werten
vorherzusagen, ist es für uns wichtig, die einzelnen Abweichungen der Punkte in
der y-Richtung möglichst klein zu halten. Wir sind also an einer
idealen Geraden interessiert, die den Vorhersagefehler möglichst minimiert.
Wir fordern für die idealisierte Gerade: die Summe der
quadrierten Abweichungen (in y-Richtung) der beobachteten von den
geschätzten Werten soll ein Minimum bilden. Wir wollen
also durch die Punkte eine Gerade durchgelegen, die am
idealsten die y-Werte schätzt.
Den Anstieg dieser Geraden und ihren Abschnitt auf
der y-Achse (die Koeffizienten b und a) lassen sich mit der Differentialrechnung
(Extremwertrechnung) ermitteln.
Wie dies im Einzelnen bestimmt wird, ist hier nicht von weiterem Interesse
und wird daher in diesem Kontext vorausgesetzt. Die Bestimmung der
Koeffizienten b und a erfolgt jedenfalls wie folgt:
Haben wir r (den Produkt-Moment-Korrelationskoeffizienten
zwischen den beiden Variablen x und y) sowie
die jeweiligen Standardabweichungen sx und sy
berechnet, so lassen sich aus diesen drei
Größen die Steigung der gewünschten Gerade b rein rechnerisch
wie folgt ermitteln:
![]()
In unserem Beispiel: r = 0.89;
sy = 2; sx = 4.47
![]() , was ungefähr 0.4 ergibt.
, was ungefähr 0.4 ergibt.
Der Abschnitt auf der y-Achse a wird so berechnet:
![]()
![]()
Daraus ergibt sich
folgende Geradengleichung:
![]()
Eigenschaften dieser Geraden und der um sie streuenden Punkte:
- Die beobachteten Werte streuen um die Gerade. Die Streuung erfolgt so, dass die Summe der quadrierten Abweichungen der beobachteten Werte zu den geschätzten Werten ein Minimum ergibt.
- Der Mittelwert der geschätzten y-Werte ist gleich dem Mittelwert
der beobachteten y-Werte (![]() )
)
- Die Varianz der beobachteten Werte ist die Summe der
Varianzen der geschätzten Werte und der Varianz der Abweichungen.
Anders gesagt: Die Abweichung eines Messwertes yi vom
Mittelwert der y-Werte (![]() ) kann in einen Anteil zerlegt werden, der
durch die Variable x "erklärt" wird (
) kann in einen Anteil zerlegt werden, der
durch die Variable x "erklärt" wird (![]() ) und einen weiteren Anteil, der bei einer Regressionsvorhersage
nicht erfasst wird (
) und einen weiteren Anteil, der bei einer Regressionsvorhersage
nicht erfasst wird (![]() ).
).
Verdeutlichen wir uns diesen wichtigen
Umstand an folgendem Beispiel:
|
x |
y |
|
|
|
|
|
3 |
3 |
-3 |
3,2 |
-2,8 |
-0,2 |
|
7 |
5 |
-1 |
4,8 |
-1,2 |
0,2 |
|
11 |
7 |
1 |
6,4 |
0,4 |
0,6 |
|
14 |
6 |
0 |
7,6 |
1,6 |
-1,6 |
|
15 |
9 |
3 |
8,0 |
2,0 |
1,0 |
s2y = 4
s2y* = 16/5 = 3,2
s2(Streuung der y-Werte um die Gerade) = 4/5 = 0,8
s2y = s2y* + s2(Streuung
der y-Werte um die Gerade)
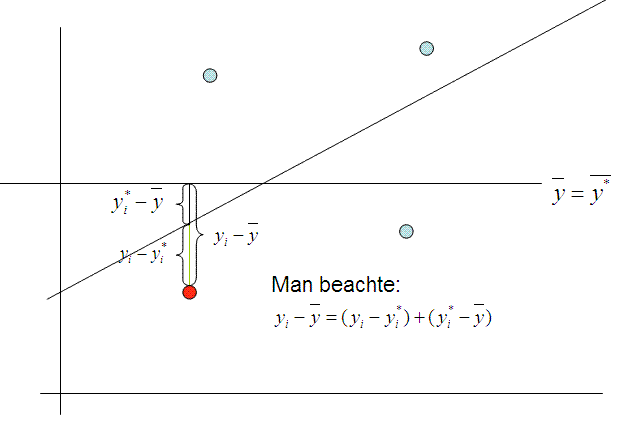
Das bedeutet: der
Abstand eines einzelnen y-Wertes vom Mittelwert der y-Werte setzt sich zusammen
aus dem Abstand dieses y-Wertes von seinem geschätzten y-Wert und dem Abstand
des geschätzten y-Wertes vom Mittelwert der y-Werte.
(Siehe auch die Tabelle oben)
Der Anteil der Varianz, der durch
die Regressionsvoraussage aufgeklärt wird, lässt sich nach der Formel
r2 * 100 (= Determinationskoeffizient)
berechnen.
r = 0,89
heißt:
0,892 * 100 = 79 % der Varianz wird durch die
Regressionsvoraussage aufgeklärt.
Das heißt anders ausgedrückt: Wie viel sind 3,2 von 4? Ca. 80%!
Ist r = 1, so werden 100% aufgeklärt (dann ist die Streuung der Punkte um die Gerade = 0)
Anhang
|
v |
Wahrscheinlichkeit |
|||||||
|
0,75 |
0,875 |
0,90 |
0,95 |
0,975 |
0,99 |
0,995 |
0,999 |
|
|
1 |
1,000 |
2,414 |
3,078 |
6,314 |
12,706 |
31,821 |
63,657 |
318,309 |
|
2 |
0,817 |
1,604 |
1,886 |
2,920 |
4,303 |
6,965 |
9,925 |
22,327 |
|
3 |
0,765 |
1,423 |
1,638 |
2,353 |
3,182 |
4,541 |
5,841 |
10,215 |
|
4 |
0,741 |
1,344 |
1,533 |
2,132 |
2,776 |
3,747 |
4,604 |
7,173 |
|
5 |
0,727 |
1,301 |
1,476 |
2,015 |
2,571 |
3,365 |
4,032 |
5,893 |
|
6 |
0,718 |
1,273 |
1,440 |
1,943 |
2,447 |
3,143 |
3,707 |
5,208 |
|
7 |
0,711 |
1,254 |
1,415 |
1,895 |
2,365 |
2,998 |
3,499 |
4,785 |
|
8 |
0,706 |
1,240 |
1,397 |
1,860 |
2,306 |
2,896 |
3,355 |
4,501 |
|
9 |
0,703 |
1,230 |
1,383 |
1,833 |
2,262 |
2,821 |
3,250 |
4,297 |
|
10 |
0,700 |
1,221 |
1,372 |
1,812 |
2,228 |
2,764 |
3,169 |
4,144 |
|
11 |
0,697 |
1,214 |
1,363 |
1,796 |
2,201 |
2,718 |
3,106 |
4,025 |
|
12 |
0,695 |
1,209 |
1,356 |
1,782 |
2,179 |
2,681 |
3,055 |
3,930 |
|
13 |
0,694 |
1,204 |
1,350 |
1,771 |
2,160 |
2,650 |
3,012 |
3,852 |
|
14 |
0,692 |
1,200 |
1,345 |
1,761 |
2,145 |
2,624 |
2,977 |
3,787 |
|
15 |
0,691 |
1,197 |
1,341 |
1,753 |
2,131 |
2,602 |
2,947 |
3,733 |
|
16 |
0,690 |
1,194 |
1,337 |
1,746 |
2,120 |
2,583 |
2,921 |
3,686 |
|
17 |
0,689 |
1,191 |
1,333 |
1,740 |
2,110 |
2,567 |
2,898 |
3,646 |
|
18 |
0,688 |
1,189 |
1,330 |
1,734 |
2,101 |
2,552 |
2,878 |
3,611 |
|
19 |
0,688 |
1,187 |
1,328 |
1,729 |
2,093 |
2,539 |
2,861 |
3,579 |
|
20 |
0,687 |
1,185 |
1,325 |
1,725 |
2,086 |
2,528 |
2,845 |
3,552 |
|
21 |
0,686 |
1,183 |
1,323 |
1,721 |
2,080 |
2,518 |
2,831 |
3,527 |
|
22 |
0,686 |
1,182 |
1,321 |
1,717 |
2,074 |
2,508 |
2,819 |
3,505 |
|
23 |
0,685 |
1,180 |
1,319 |
1,714 |
2,069 |
2,500 |
2,807 |
3,485 |
|
24 |
0,685 |
1,179 |
1,318 |
1,711 |
2,064 |
2,492 |
2,797 |
3,467 |
|
25 |
0,684 |
1,178 |
1,316 |
1,708 |
2,060 |
2,485 |
2,787 |
3,450 |
|
26 |
0,684 |
1,177 |
1,315 |
1,706 |
2,056 |
2,479 |
2,779 |
3,435 |
|
27 |
0,684 |
1,176 |
1,314 |
1,703 |
2,052 |
2,473 |
2,771 |
3,421 |
|
28 |
0,683 |
1,175 |
1,313 |
1,701 |
2,048 |
2,467 |
2,763 |
3,408 |
|
29 |
0,683 |
1,174 |
1.311 |
1.699 |
2.045 |
2.462 |
2.756 |
3.396 |
|
30 |
0,683 |
1,173 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
3,385 |
|
40 |
0,681 |
1,167 |
1,303 |
1,684 |
2,021 |
2,423 |
2,704 |
3,307 |
|
50 |
0,679 |
1,164 |
1,299 |
1,676 |
2,009 |
2,403 |
2,678 |
3,261 |
|
60 |
0,679 |
1,162 |
1,296 |
1,671 |
2,000 |
2,390 |
2,660 |
3,232 |
|
70 |
0,678 |
1,160 |
1,294 |
1,667 |
1,994 |
2,381 |
2,648 |
3,211 |
|
80 |
0,678 |
1,159 |
1,292 |
1,664 |
1,990 |
2,374 |
2,639 |
3,195 |
|
90 |
0,677 |
1,158 |
1,291 |
1,662 |
1,987 |
2,368 |
2,632 |
3,183 |
|
100 |
0,677 |
1,157 |
1,290 |
1,660 |
1,984 |
2,364 |
2,626 |
3,174 |
|
200 |
0,676 |
1,154 |
1,286 |
1,653 |
1,972 |
2,345 |
2,601 |
3,131 |
|
300 |
-- |
-- |
1,284 |
1,650 |
1,968 |
2,339 |
2,592 |
3,118 |
|
400 |
-- |
-- |
1,284 |
1,649 |
1,966 |
2,336 |
2,588 |
3,111 |
|
500 |
0,675 |
1,152 |
1,283 |
1,648 |
1,965 |
2,334 |
2,586 |
3,107 |
|
∞ |
0,674 |
1,150 |
1,282 |
1,645 |
1,960 |
2,326 |
2,576 |
3,090 |
Von „http://de.wikipedia.org/wiki/Students_t-Verteilung“