Probleme bei kleinen Stichprobenumfängen und t-Verteilung
Fassen wir zusammen: Wir sind bisher von der Frage ausgegangen, mit welcher Wahrscheinlichkeit der Mittelwert einer empirischen Stichprobe vom Mittelwert µ0 in einer Population abweicht. Um diese Wahrscheinlichkeit quantifizieren zu können, mussten wir davon ausgehen, dass die Stichprobenkennwertverteilung der Mittelwerte normalverteilt ist. Zur Stützung dieser Annahme verwendeten wir das zentrale Grenztheorem, demzufolge sich die Mittelwertsverteilung bei großem Stichprobenumfang einer Normalverteilung annähert. Großer Stichprobenumfang bedeutet in der Praxis: n ≥ 30.
Was ist nun aber zu tun, wenn unsere Stichprobe aus einem n < 30 besteht? Da in diesem Falle das zentrale Grenzwerttheorem nicht zum Tragen kommt, können wir nicht von vornherein annehmen, dass die Kennwertverteilung der Mittelwerte normalverteilt ist. Nun ist aber die Annahme der Normalverteilung für die Stichprobenkennwertverteilung eine unabdingbare Voraussetzung für unser wahrscheinlichkeitstheoretisches Schlussverfahren.
Die Frage ist: Können wir Bedingungen angeben, unter denen auch bei kleinerem n die Kennwertverteilung normalverteilt ist? Die Antwort darauf ist schlicht: Ja.
Unter der Voraussetzung nämlich, dass die Daten in der Population selbst normalverteilt sind und unter der weiteren Voraussetzung, dass die Streuung σ in der Population bekannt ist, ist auch bei kleinerem n die Kennwertverteilung normalverteilt. Diese Zusatzbedingungen - Normalverteilung in der Population und Bekanntheit von σ - ist bei größerem N wegen des zentralen Grenzwerttheorems verzichtbar.
Nochmals zusammengefasst: Sind die Daten in einer Population mit bekanntem σ normalverteilt, so kann man auch bei kleinerem N für die Kennwertverteilung von einer z-Transformation Gebrauch machen.
(zur Erinnerung: durch die z-Transformation wird eine Normalverteilung in eine Standardnormalverteilung transformiert)
Was ist aber zu tun, wenn die Standardabweichung der Daten in der Population nicht bekannt ist?
Zur Erinnerung:
![]()
Der z-Wert ist nichts anderes als der Quotient (Bruch) von Mittelwertsdifferenz und Standardfehler des Mittelwertes.
Der Standardfehler des Mittelwertes berechnet sich nach der Formel:
![]()
Ist σ keine Schätzung aus der Stichprobe, sondern eine von der Population her bekannte Größe, so ergibt sich daraus: Zwei verschiedene Stichproben mit dem gleichen Mittelwert haben auch den gleichen z-Wert bzw. den gleichen Quotienten von Mittelwertsdifferenz und Standardfehler des Mittelwertes!
Nun ist aber in der Praxis die Populationsvarianz nicht bekannt, sondern muss aus der Stichprobenvarianz geschätzt werden. Das bedeutet aber: Zwei verschiedene Stichproben mit dem gleichem Mittelwert können einen verschiedenen Quotienten haben!
Nun gilt aber: Ist die Populationsvarianz nicht bekannt, sondern eine Schätzung aus der Stichprobe, so erhält man statt eines z-Wertes einen so genannten t-Wert, also:
![]()
Aufgrund der vorangehenden Überlegungen gilt aber: Zwei Stichproben mit dem gleichen Mittelwert können einen verschiedenen t-Wert haben.
Betrachtet man nicht nur den t-Wert einer Stichprobe, sondern die t-Werte der gesamten Stichprobenverteilung, so erhält man die so genannte t-Verteilung.
Diese t-Verteilung ähnelt in ihrer Form der Normalverteilung, ist aber flacher und an beiden Enden breiter
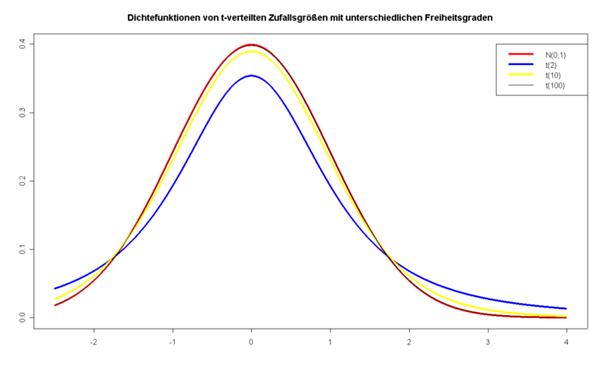
Quelle: wikipedia.de
Die Überschreitungswahrscheinlichkeit für extreme t-Werte ist größer als für die entsprechenden z-Werte. Dies führt dazu, dass hohe Abweichungen unterschätzt werden. Die Nullhypothese wird daher bei t-Werten nicht so schnell verworfen. Bekannt ist die t-Verteilung auch unter dem Namen "Student's t Verteilung". Dieser Name stammt von W.S. Gosset, der diese Verteilung erstmalig 1908 unter dem Pseudonym "Student" veröffentlichte.
Nun gilt weiters: Bei großem N wird die Schätzung der Populationsvarianz durch die Stichprobenvarianz immer besser bzw. nähert sich der Populationsvarianz. In diesem Falle geht die t-Verteilung in die z-Verteilung über und wir können in diesem Falle so vorgehen, wie bereits bei der z-Transformation besprochen. Wir können also die t-Werte wie z-Werte behandeln.
Wie verhält sich dies nun aber im Falle kleinerer Stichprobenumfänge? In diesem Falle müssen wir die Wahrscheinlichkeiten für unseren Quotienten statt in der Standardnormalverteilungstabelle in der t-Verteilungstabelle nachschlagen. Voraussetzung dafür, um das überhaupt tun zu können, ist allerdings, dass die Daten in der Population normalverteilt sind.
Überlegungen wir uns zunächst, wie wir (beispielsweise bei einer einseitigen Fragestellung) bei der z-Verteilung vorgegangen sind. Wir berechneten zunächst aufgrund des Mittelwertes der Stichprobe den z-Wert. Dieser z-Wert wurde dann anschließend mit dem zkritisch verglichen. zkritisch liegt bei einseitiger Fragestellung und einem Signifikanzniveau von 5% bei z=1,65
Die Frage ist nun: Wo liegt tkritisch - ebenfalls bei einseitiger Fragestellung und einem Signifikanzniveau von 5%?
Da - wie wir bereits wissen - Stichproben mit gleichem Mittelwert einen verschiedenen t-Wert haben können, hängt unser tkritisch von der Stichprobenvarianz ab. Diese Stichprobenvarianz wiederum ist vom Stichprobenumfang abhängig. Große Stichproben nähern sich der Populationsvarianz, kleinere verschätzen sie eher.
Wir erhalten die Schätzung der Populationsvarianz, indem wir die Quadratsumme der Abweichungen vom Stichprobenmittelwert durch N-1 dividieren.
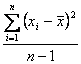
Die Anzahl N-1 wird auch als Anzahl der Freiheitsgrade der Varianz bezeichnet. Was dies bedeutet, zeigt die folgende Überlegung: Zur Berechnung der Varianz benötigen wir die Summe der Abweichungen vom Mittelwert. Diese muss, wie wir bereits wissen, Null ergeben. Nehmen wir nun an, unser N sei gleich 4. Die Differenzen der ersten drei Messwerte zum Mittelwert seien 6, -9 und -7. Da die Summe aller 4 Differenzen Null ergeben muss, ist die vierte Differenz festgelegt. Allgemein gilt: Kennen wir N-1 Abweichungen zum Mittelwert, so ist auch die N-te Differenz festgelegt. Wir haben also nur N -1 Freiheitsgrade zur Festlegung der Varianz.
Von der Anzahl der Freiheitsgrade hängt nun aber wiederum unser tkritisch ab: Bei beispielsweise 20 Freiheitsgraden (siehe t-Tabelle) beträgt bei einem Signifikanzniveau von 5% tkritisch = 1,725. Dieses tkritisch nähert sich bei Erhöhung der Freiheitsgrade immer mehr dem entsprechenden zkritisch von 1,65!
Abschließend zur Verwendung der t-Verteilung:
1) Wird verwendet, wenn die Populationsvarianz aus der Stichprobenvarianz geschätzt werden muss
2) Bei kleinem N nachschauen in t-Tabelle. Voraussetzung ist aber Normalverteilung der Population.
Bei großem N verfahre wie im Falle der z-Tabelle.
3) Berechnung von terrechnet. Gleiche Formel wie das entsprechende z.
4) Vergleiche terrechnet mit tkritisch. tkritisch wird der t-Verteilungstabelle entnommen - Man beachte die Anzahl der Freiheitsgrade = N - 1.
5) Ist |terrechnet| ≥ |tkritisch| -> Verwerfung der H0
t-Verteilung
|
v |
Wahrscheinlichkeit |
|||||||
|
0,75 |
0,875 |
0,90 |
0,95 |
0,975 |
0,99 |
0,995 |
0,999 |
|
|
1 |
1,000 |
2,414 |
3,078 |
6,314 |
12,706 |
31,821 |
63,657 |
318,309 |
|
2 |
0,817 |
1,604 |
1,886 |
2,920 |
4,303 |
6,965 |
9,925 |
22,327 |
|
3 |
0,765 |
1,423 |
1,638 |
2,353 |
3,182 |
4,541 |
5,841 |
10,215 |
|
4 |
0,741 |
1,344 |
1,533 |
2,132 |
2,776 |
3,747 |
4,604 |
7,173 |
|
5 |
0,727 |
1,301 |
1,476 |
2,015 |
2,571 |
3,365 |
4,032 |
5,893 |
|
6 |
0,718 |
1,273 |
1,440 |
1,943 |
2,447 |
3,143 |
3,707 |
5,208 |
|
7 |
0,711 |
1,254 |
1,415 |
1,895 |
2,365 |
2,998 |
3,499 |
4,785 |
|
8 |
0,706 |
1,240 |
1,397 |
1,860 |
2,306 |
2,896 |
3,355 |
4,501 |
|
9 |
0,703 |
1,230 |
1,383 |
1,833 |
2,262 |
2,821 |
3,250 |
4,297 |
|
10 |
0,700 |
1,221 |
1,372 |
1,812 |
2,228 |
2,764 |
3,169 |
4,144 |
|
11 |
0,697 |
1,214 |
1,363 |
1,796 |
2,201 |
2,718 |
3,106 |
4,025 |
|
12 |
0,695 |
1,209 |
1,356 |
1,782 |
2,179 |
2,681 |
3,055 |
3,930 |
|
13 |
0,694 |
1,204 |
1,350 |
1,771 |
2,160 |
2,650 |
3,012 |
3,852 |
|
14 |
0,692 |
1,200 |
1,345 |
1,761 |
2,145 |
2,624 |
2,977 |
3,787 |
|
15 |
0,691 |
1,197 |
1,341 |
1,753 |
2,131 |
2,602 |
2,947 |
3,733 |
|
16 |
0,690 |
1,194 |
1,337 |
1,746 |
2,120 |
2,583 |
2,921 |
3,686 |
|
17 |
0,689 |
1,191 |
1,333 |
1,740 |
2,110 |
2,567 |
2,898 |
3,646 |
|
18 |
0,688 |
1,189 |
1,330 |
1,734 |
2,101 |
2,552 |
2,878 |
3,611 |
|
19 |
0,688 |
1,187 |
1,328 |
1,729 |
2,093 |
2,539 |
2,861 |
3,579 |
|
20 |
0,687 |
1,185 |
1,325 |
1,725 |
2,086 |
2,528 |
2,845 |
3,552 |
|
21 |
0,686 |
1,183 |
1,323 |
1,721 |
2,080 |
2,518 |
2,831 |
3,527 |
|
22 |
0,686 |
1,182 |
1,321 |
1,717 |
2,074 |
2,508 |
2,819 |
3,505 |
|
23 |
0,685 |
1,180 |
1,319 |
1,714 |
2,069 |
2,500 |
2,807 |
3,485 |
|
24 |
0,685 |
1,179 |
1,318 |
1,711 |
2,064 |
2,492 |
2,797 |
3,467 |
|
25 |
0,684 |
1,178 |
1,316 |
1,708 |
2,060 |
2,485 |
2,787 |
3,450 |
|
26 |
0,684 |
1,177 |
1,315 |
1,706 |
2,056 |
2,479 |
2,779 |
3,435 |
|
27 |
0,684 |
1,176 |
1,314 |
1,703 |
2,052 |
2,473 |
2,771 |
3,421 |
|
28 |
0,683 |
1,175 |
1,313 |
1,701 |
2,048 |
2,467 |
2,763 |
3,408 |
|
29 |
0,683 |
1,174 |
1.311 |
1.699 |
2.045 |
2.462 |
2.756 |
3.396 |
|
30 |
0,683 |
1,173 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
3,385 |
|
40 |
0,681 |
1,167 |
1,303 |
1,684 |
2,021 |
2,423 |
2,704 |
3,307 |
|
50 |
0,679 |
1,164 |
1,299 |
1,676 |
2,009 |
2,403 |
2,678 |
3,261 |
|
60 |
0,679 |
1,162 |
1,296 |
1,671 |
2,000 |
2,390 |
2,660 |
3,232 |
|
70 |
0,678 |
1,160 |
1,294 |
1,667 |
1,994 |
2,381 |
2,648 |
3,211 |
|
80 |
0,678 |
1,159 |
1,292 |
1,664 |
1,990 |
2,374 |
2,639 |
3,195 |
|
90 |
0,677 |
1,158 |
1,291 |
1,662 |
1,987 |
2,368 |
2,632 |
3,183 |
|
100 |
0,677 |
1,157 |
1,290 |
1,660 |
1,984 |
2,364 |
2,626 |
3,174 |
|
200 |
0,676 |
1,154 |
1,286 |
1,653 |
1,972 |
2,345 |
2,601 |
3,131 |
|
300 |
-- |
-- |
1,284 |
1,650 |
1,968 |
2,339 |
2,592 |
3,118 |
|
400 |
-- |
-- |
1,284 |
1,649 |
1,966 |
2,336 |
2,588 |
3,111 |
|
500 |
0,675 |
1,152 |
1,283 |
1,648 |
1,965 |
2,334 |
2,586 |
3,107 |
|
∞ |
0,674 |
1,150 |
1,282 |
1,645 |
1,960 |
2,326 |
2,576 |
3,090 |
Von „http://de.wikipedia.org/wiki/Students_t-Verteilung“