Grundprinzipien der Inferenzstatistik am Beispiel der Binomialverteilung

 

 

Gehen  wir von einer konkreten Stichprobe aus: Es wurde 20-mal hintereinander gewürfelt und dabei 10-mal eine sechs erzielt. Die 20 Würfe sind die Stichprobe eines Bernoulli-Prozesses. Zur Erinnerung:  Ein Bernoulli-Prozess ist ein Experiment mit zwei  möglichen  Ausgängen (Erfolg und Misserfolg). Nun habe unsere  empirisch erhobene Stichprobe ein Ergebnis von 10-mal Erfolg bei 20 Bernoulli-Versuchen  erbracht. Dies ist nur  ein mögliches Ergebnis. Prinzipiell können bei 20  Versuchen insgesamt 21 verschiedene mögliche Stichprobenergebnisse vorkommen. Diese sind: 0-mal Erfolg bei 20 Würfen; 1-mal Erfolg usw. bis 20-mal Erfolg.

Was  wir  als nächstes für  unser  inferenzstatistisches Schließen benötigen,  ist  eine Hypothese. Gehen wir fürs erste von  der  rein hypothetischen Annahme aus, in "Wahrheit" sei die Wahrscheinlichkeit  für Erfolg (= eine sechs zu würfeln) 1/6.  Die  Wahrscheinlichkeit  für  Misserfolg ergibt sich daraus implizit  -  sie beträgt  5/6. Dies ist zunächst nur  eine  hypothetische Annahme.  Diese Annahme wurde im einführenden Teil als  die Unschuldsbehauptung bezeichnet. In der Inferenzstatistik  bezeichnet man die Unschuldsbehauptung  als so genannte Nullhypothese.

Grundsätzlich sind drei  Begriffe zu unterscheiden:  die Stichprobe, die  Stichprobenkennwertverteilung (dies ist die Verteilung der Wahrscheinlichkeiten für die verschiedenen Stichprobenergebnisse; im Falle der Binomialverteilung die Wahrscheinlichkeiten für die verschiedenen k's) und die Grundgesamtheit (=Population).

Die Grundgesamtheit ist das Ergebnis (= der Ausgang) aller möglicher  Bernoulli-Versuche mit einem Würfel, wobei wir nur  an  den beiden  Ausgängen Erfolg oder nicht Erfolg interessiert sind.  Würden  alle Ergebnisse von vornherein feststehen, bzw. würden wir die  Population  bereits kennen, so benötigten wir keine  Inferenzstatistik.

Was ist nun die Stichprobe? Die Stichprobe besteht aus den 20 Bernoulli-Versuchen. Die  Stichprobenkennwerteverteilung wiederum besteht aus den Wahrscheinlichkeiten für die  21 verschiedenen möglichen Stichprobenergebnisse:  0 gewürfelte Sechser bei 20 Versuchen, 1 Sechser  bis zu 20 Sechser bei  20 Versuchen. Die Wahrscheinlichkeiten werden mit der Wahrscheinlichkeitsfunktion der Binomialverteilung ermittelt.

 

Die zentrale Frage, die sich nun stellt, ist die folgende: Inwiefern  lässt  sich  unsere hypothetische Annahme,  dass  nämlich  die Wahrscheinlichkeit  für Erfolg 1/6 ist, durch  unsere  empirische Stichprobe bestätigen?

Anders  formuliert:  Inwiefern  verträgt  sich  unser  empirisch ermitteltes  Stichprobenergebnis - Würfeln von 10 6ern bei  insgesamt  20 Versuchen - mit unserer Hypothese? Unserer Hypothese zufolge  handelt es sich bei dem Würfel um einen 'fairen' Würfel - die Wahrscheinlichkeit, eine sechs zu bekommen beträgt dieser Hypothese zufolge also 1/6! 

 

Überlegen wir uns diese Frage an zwei Beispielen: Wenn  wir statt 10 6ern nur 3 bekommen hätten, wie verträgt sich dieses Ergebnis  mit unserer Theorie? Wie groß wäre die  Wahrscheinlichkeit 3-mal eine sechs zu bekommen bei 20 Versuchen? Aufgrund  der Wahrscheinlichkeitsfunktion  der  Binomialverteilung  können  wir dafür  die Wahrscheinlichkeit berechnen. Diese ist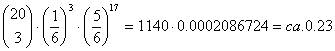

 

Zweites Beispiel: Wie groß wäre die Wahrscheinlichkeit, 4-mal bei 20 Würfen eine sechs zu bekommen? Diese ist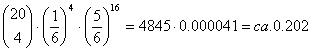

Hätten  wir  aufgrund  von 3 oder 4maligem  Würfeln  einer  sechs also Anlass, an der Unschuldsbehauptung zu zweifeln? Nachdem die  Wahrscheinlichkeiten  dieser Ergebnisse in der  Stichprobenverteilung relativ  hoch sind, hätten wir aufgrund dieser  Ergebnisse  wenig Anlass, an der Unschuldsbehauptung zu zweifeln.

 

Betrachten  wir  nun aber unseren konkreten Fall:  Bei  20maligem Würfeln  10-mal eine sechs zu bekommen.  Die  Wahrscheinlichkeit dafür  berechnet sich nach der Formel:

 

 

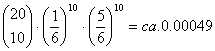
Nun spricht die Wahrscheinlichkeit dieses Ergebnis  nicht  gerade dafür, dass die  Nullhypothese  zutrifft. Unser empirisch ermittelter Befund scheint nicht die Unschuldsbehauptung  zu  stützen. Wir können aber aufgrund dieses Ergebnisses umgekehrt  auch nicht völlig sicher sein, dass  die  Nullhypothese falsch ist. Das erzielte Ergebnis ist zwar unwahrscheinlich, aber nicht  unmöglich.  Aufgrund welcher Kriterien  können  wir  daher behaupten,  dass die Nullhypothese falsch ist? Da das  beobachtete Ergebnis zwar unwahrscheinlich, aber nicht unmöglich ist,  gehen wir  in  jedem Falle ein Risiko ein, wenn wir  die  Nullhypothese verwerfen. Wie können wir dieses Risiko möglichst gering  halten? Dazu müssen wir die Wahrscheinlichkeit wissen fälschlicherweise die Nullhypothese zu verwerfen. Diese Wahrscheinlichkeit finden wir über die Überschreitungswahrscheinlichkeit. Dazu folgende Überlegung:

Angenommen, wir entscheiden uns aufgrund der geringen Wahrscheinlichkeit dieses Ergebnisses gegen die Nullhypothese.  Angenommen, wir sagen, 10-mal eine sechs bei 20 Versuchen ist zu unwahrscheinlich. Würden wir  im  Falle einer derartigen Entscheidung das  Werfen  von  11 6ern akzeptieren? Die Antwort darauf ist ein klares Nein, denn wenn 10 zu viel sind, dann wären auch 11, 12, 13, 14 bis zu 20-mal zu viel. In all diesen Fällen würden wir  also die Nullhypothese verwerfen. Wir kommen hier  zu  einem wichtigen Punkt der Inferenzstatistik: Man kann nicht 10-mal Würfeln einer sechs als zu unwahrscheinlich verwerfen und dann aber  11-mal  Würfeln akzeptieren. Nachdem aber 10-mal und mehr  verworfen wird, müssen wir die Überschreitungswahrscheinlichkeit berechnen. Dies ist die Gesamtwahrscheinlichkeit, 10mal, 11mal bis zu 20mal eine 6 zu bekommen. Betrachten wir dazu die Ergebnisse der Binomialverteilung:

 

k = 10 -> P = 0,00049

k = 11 -> P = 0,000089

k = 12 -> P = 0,000013

k = 13 -> P = 0,000001

k = 14 -> P = 0,0000001

k = 15 -> P = praktisch 0

k = 16 -> P = praktisch 0

k = 17 -> P = praktisch 0

k = 18 -> P = praktisch 0

k = 19 -> P = praktisch 0

k = 20 -> P = praktisch 0

 

Dies  ergibt in der Summe eine  Überschreitungswahrscheinlichkeit von ca. 0,001!

Das  bedeutet:  Das Risiko, fälschlicherweise  die  Nullhypothese (dass  unser Würfel fair ist bzw. dass p=1/6) bei 10-maligem Werfen der Augenzahl 6 zu  verwerfen,  tritt mit einer Wahrscheinlichkeit von 0,001 auf. Das bedeutet  weiterhin:  Ein Stichprobenergebnis von 10 oder mehr  Sechsern  liefert wenig  Evidenz  für unsere Hypothese. Nochmals  anders  formuliert: Unter der Voraussetzung der Nullhypothese ist das Ergebnis  unserer empirischen Stichprobe sehr unwahrscheinlich.

 

Wie wir bereits wissen, lässt sich die Überschreitungswahrscheinlichkeit auch angenähert über die z-Transformation berechnen. Dies allerdings nur unter der Voraussetzung, dass unser n hinreichend groß ist – was bei 20 Versuchen nicht der Fall ist.

Obwohl diese Bedingung bei 20 Versuchen also nicht gegeben ist, versuchen wir allein aus Demonstrationszwecken und zur Gegenüberstellung zur oben verwendeten Berechnungsart im folgenden mit  Hilfe der Approximation an eine Normalverteilung die Wahrscheinlichkeit berechnen, 10 mal oder mehr eine 6 zu bekommen.

Fragen  wir  zunächst nach der Wahrscheinlichkeit, bis zu  10-mal eine  sechs  zu bekommen. Da 10 in diesem Falle  als  Klassenmitte einer  kontinuierlichen  Variablen  aufgefasst  wird, beginnt deren Klassenuntergrenze tatsächlich bei 9,5. Um dann die Wahrscheinlichkeit 10 mal oder mehr eine 6 zu bekommen zu erhalten, müssen  wir die Wahrscheinlichkeit von -unendlich bis 9,5 berechnen und die erhaltene Wahrscheinlichkeit dann von 1 subtrahieren. Mit Hilfe der z-Transformation erhalten wir:

 

_,

 

Aufgrund der z-Tabelle ergibt sich daraus eine Wahrscheinlichkeit von: 0,9999

Die  Überschreitungswahrscheinlichkeit   (die Wahrscheinlichkeit  10-mal oder mehr eine 6 zu  bekommen)  liegt daher bei 1 – 0,999, also bei 0,000000... Das Risiko, die Nullhypothese zu verwerfen, ist demnach sehr klein.

 

Was jetzt  noch offen geblieben ist, ist die Frage,  ab  welcher Überschreitungswahrscheinlichkeit  wir  die  Nullhypothese  verwerfen sollen. Diese muss so gewählt werden, dass das Risiko, die  Nullhypothese  fälschlicherweise zu verwerfen, möglichst klein  gehalten wird. In den Sozialwissenschaften hat sich dabei folgende Konvention  ergeben: Ist die Überschreitungswahrscheinlichkeit für  die  Nullhypothese kleiner als 0,05, so entscheidet man sich gegen die  Nullhypothese. Man bezeichnet diese Schwelle auch als Signifikanzniveau. Man geht  dabei  von der Überlegung aus, dass ein  derart  empirisch erhobener Befund unter Voraussetzung der Nullhypothese grundsätzlich zwar möglich, aber eben doch sehr unwahrscheinlich ist.

In  Bezug  auf unsere konkrete Nullhypothese, dass  nämlich  unser Würfel  ein fairer Würfel ist, können wir nun folgende  Entscheidungsregeln festhalten:

 

H₀: π = 1/6

H₁: π > 1/6 (die Wahrscheinlichkeit für "6" ist größer als 1/6)

H₁ bezeichnet man auch als Alternativhypothese.

 

Ergibt sich aufgrund der Binomialverteilung eine Überschreitungswahrscheinlichkeit kleiner  gleich 0,05,  so  entscheidet man sich gegen die  Nullhypothese.  Anders formuliert: Aufgrund einer derart kleinen  Irrtumswahrscheinlichkeit  kann die Nullhypothese nicht weiter aufrecht gehalten  werden. Entscheidet man sich gegen die Nullhypothese, so spricht man auch von einem signifikanten Ergebnis.