Der Vergleich eines Stichprobenmittelwertes mit einem
Populationsmittelwert
Am Beispiel des Falschspielers haben wir - unterstützt durch Kenntnisse über die Eigenschaften der Binomialverteilung - erstmals gesehen, welchen Grundprinzipien das inferenzstatistische Schließen folgt. Im Folgenden geht es darum, diese allgemeinen Überlegungen auf eine konkrete Fragestellung in der Psychologie zu übertragen. Weder Würfeln noch das Werfen einer Münze gehören zu den typischen Fragen in der Psychologie, die Beispiele dienten lediglich dem Zweck, eine Brücke zur Inferenzstatistik zu schlagen. Eine typische Fragestellung in der Psychologie ist beispielsweise die folgende: 30 Probanden wurde in einem Experiment ein bestimmtes Medikament verabreicht. Gefragt wird, inwiefern dieses Medikament das Verhalten im Straßenverkehr tatsächlich beeinflusst.
Gehen wir weiters im Folgenden der Einfachheit halber davon aus, dass für die Reaktionszeit bestimmte Normen vorliegen. Wir messen also die Reaktionszeit an einem standardisierten Gerät und erhalten einen bestimmten Mittelwert und eine Standardabweichung für eine Norm-Stichprobe. Nehmen wir an, der Mittelwert in der Normstichprobe sei 100 ms und die Standardweichung in der Normstichprobe sei 20 ms. Nehmen wir weiters an, in unserer empirisch ermittelten Stichprobe hätten wir einen Stichprobenmittelwert von 105 ms bekommen. Es stellt sich nun grundsätzlich die folgende Frage: Inwiefern lässt sich die Nullhypothese, dass nämlich der tatsächliche Mittelwert (wie in der Normstichprobe) 100 ms beträgt, mit unserer empirisch ermittelten Stichprobe, nämlich einem Mittelwert von 105 ms vereinbaren?
Die Nullhypothese (die H0) besagt in diesem Falle: Der Mittelwert von Probanden, die das Medikament verabreicht bekommen haben, stammt aus einer Population mit einem Mittelwert von µ=100. Die Abweichung des empirisch ermittelten Mittelwertes ist rein zufälliger Natur.
Die Alternativhypothese (H1) besagt: Die Reaktionszeit verlangsamt sich nach Einnahme des Medikaments. Eine derartige Abweichung des empirisch ermittelten Mittelwerts von dem Mittelwert in der Normstichprobe wäre unter Geltung der H0 sehr unwahrscheinlich. Wir entscheiden uns in diesem Falle gegen die Nullhypothese und für die Alternativhypothese. (Signifikanzniveau sei wiederum p= 0,05).
Um die eigentliche Logik der in diesem Falle wirksam werdenden inferenzstatistischen Regeln zu verstehen, müssen wir - in Analogie zum Beispiel des Falschspielers - drei Begriffe auseinander halten, nämlich: 1) die Grundgesamtheit 2) die Stichprobe 3) die Stichprobenkennwerteverteilung
ad 1) Unter der Grundgesamtheit (=Population) verstehen wir alle potentiellen Beobachtungseinheiten, bei den eine oder mehrere Eigenschaften gemessen wurden. In vielen Fällen handelt es sich in der Psychologie bei den Beobachtungseinheiten konkret um Personen und die gemessenen Merkmale sind eben Eigenschaften dieser Personen. Beispiel: Intelligenz, Reaktionszeit usw. Im Falle eines Bernoulli-Versuches handelt es sich bei der Grundgesamtheit - zur Erinnerung - um die Menge aller möglichen Ausgänge eines Bernoulli-Versuches.
Der Mittelwert eines bestimmten Merkmals in der Population wird mit dem griechischen Buchstaben µ bezeichnet; die Standardabweichung mit dem griechischen Buchstaben σ.
.
ad 2) Was ist im konkret vorliegenden Falle unter der Stichprobe zu verstehen?
Unter einer Stichprobe versteht man im konkreten Fall die erhobenen Daten, also unsere Reaktionszeiten gemessen an 30 Probanden.
In der Inferenzstastik geht man meistens davon aus, dass es sich bei der Stichprobe um eine so genannte Zufallstichprobe handelt. Das bedeutet, dass die Wahrscheinlichkeit für jede Untersuchungseinheit der Population, in unserer Stichprobe vorzukommen, gleich groß ist. Wie kommen wir aber zu einer Zufallsstichprobe? Stellen Sie sich vor, Sie hätten ein Verzeichnis aller Bürger der Vereinigten Staaten und würden daraus rein zufällig 30 Personen auswählen. Das Problem selbst bei einer derartigen Zufallstichprobe ist nun aber, dass die Grundgesamtheit sich auf die Bürger der Vereinigten Staaten einschränkt und dabei spezielle Eigenschaften aufweisen könnten, die Versuchspersonen anderer Staaten nicht aufweisen. Ein weiteres Problem bei der Erhebung einer Zufallsstichprobe besteht darin, dass wir unsere Aussagen auch auf potentielle Untersuchungseinheiten ausdehnen wollen - auf Untersuchungseinheiten, die vielleicht erst in der Zukunft auftreten. Eine Änderung der Reaktionszeit bei Verabreichung eines Medikaments kann auch bei Probanden auftreten, die noch nicht geboren sind.
Wie man sieht, ist es in der Praxis nicht so einfach, eine Zufallsstichprobe zu bekommen. Gelegentlich wird auch eine so genannte proportional geschichtete Stichprobe verwendet. Angenommen, Sie kennen den proportionalen Anteil des Geschlechts in der Grundgesamtheit. Um nun eine repräsentative Stichprobe zu bekommen, wählen Sie in ihrer Stichprobe den gleichen Anteil.
In den im folgenden Teil besprochenen Verfahren gehen wir allerdings davon aus, dass es sich bei unserer Stichprobe um eine Zufallsstichprobe handelt.
ad 3) Stichprobenkennwerteverteilung
Unter einem statistischen Kennwert verstehen wir irgendeine Statistik, die wir aufgrund einer bestimmten Stichprobe berechnen können. Wir haben bereits im WS eine Reihe von verschiedenen statistischen Kennwerten kennen gelernt: Maße der zentralen Tendenz (Mittelwert, Median, Modalwert) und Dispersionsmaße (Variationsbreite, Interquartilbereich, Varianz). Prinzipiell sind den Möglichkeiten an Berechnung von statistischen. Kennwerten keine Grenzen gesetzt. So könnte man beispielsweise bei jeder Stichprobe einfach die Messung der zweiten Untersuchungseinheit herausgreifen, oder einfach die Summe aller Messergebnisse berechnen usw.
Nicht jede dieser Statistiken enthält aber das gleiche Ausmaß an Informationen über die Stichprobe. So fließt beispielsweise in die Berechnung des Median weniger Informationen über unsere Daten ein als im Falle der Berechnung eines Mittelwertes. Der Mittelwert erfasst - im Unterschied zum Median - auch Ausreißer. Zur Veranschaulichung betrachten wir hierzu folgende Daten:
1, 3, 4, 5, 7
Der Median dieser Daten ist - ungerade Gesamtanzahl! - gleich dem Wert 4.
An diesem Wert ändert sich auch nichts, wenn wir den letzten Wert unserer Datenreihe von 7 auf 1000 abändern:
Der Median der Datenreihe 1, 3, 4, 5, 1000 ist ebenfalls 4!
Das liegt daran, dass der Median nur jene Informationen in den Daten berücksichtigt, die in einer Ordinalskala enthalten sind.
Im Unterschied zum Median ändert sich dahingegen der Mittelwert gewaltig, wenn wir den letzten Wert von 7 auf 1000 abändern. Das liegt daran, dass der Mittelwert auch die Abstände zwischen den Werten mitberücksichtigt. Kurz: In den Mittelwert fließen mehr Informationen über unsere Daten ein als in den Median.
Zu beachten ist dabei allerdings, dass die Daten intervallskaliert sind, da nur in diesem Falle der Mittelwert berechnet werden kann.
Da es verschiedene statistische Kennwerte gibt, stellt sich die Frage, nach welchen Kriterien wir den sinnvollsten statistischen Kennwert auswählen sollen.
Ein wesentliches Kriterium ist, inwiefern ein statistischer Kennwert uns etwas über die Verteilung in der Grundgesamtheit sagen kann. Anders formuliert:
Inwiefern ist
der statistische Kennwert
eine gute Schätzung
des entsprechenden Kennwertes in der Grundgesamtheit?
Man geht nach drei Kriterien vor: statistische Kennwerte können
a) erwartungstreue b) konsistente und c) effiziente Schätzwerte des Kennwertes in der Grundgesamtheit sein.
ad a) Betrachten wir hierzu als Beispiel vorerst nur den Mittelwert
Entnehmen wir aus einer Grundgesamtheit immer wieder verschiedene Stichproben (mit beispielsweise je 30 Beobachtungseinheiten), so erhalten wir für jede dieser Stichproben je einen verschiedenen Mittelwert. Betrachten wir nun die Verteilung dieser verschiedenen Stichprobenmittelwerte, so haben wir ein typisches Beispiel für eine Stichprobenkennwerteverteilung. Jedem Mittelwert dieser Verteilung entspricht eine bestimmte Wahrscheinlichkeit (genauer: Wahrscheinlichkeitsdichte)
Für
den Mittelwert lässt sich nun die
folgende statistische Eigenschaft nachweisen. Bezeichnen wir den
Mittelwert einer bestimmten Variable in der Gesamtpopulation mit µ. Entnehmen
wir nun dieser Gesamtpopulation unendlich
viele Stichproben der Größe N und
berechnen für jeden dieser Stichproben den Mittelwert![]() , so gilt: der durchschnittliche Wert aller
, so gilt: der durchschnittliche Wert aller ![]() -Werte ist exakt gleich µ!
-Werte ist exakt gleich µ!
Der Mittelwert einer Stichprobe wird daher als unverzerrte Schätzung des Populationsmittelwertes angesehen. Anders formuliert bedeutet das:
der Mittelwert ist ein erwartungstreuer Parameter des Populationsmittelwertes.
Allgemein gilt: Ist der durchschnittliche Wert einer Stichprobenkennwerteverteilung exakt gleich dem Kennwert in der Population, so wird der Kennwert als erwartungstreue Schätzung bezeichnet.
Ganz anders verhält es sich mit der Varianz:
Entnehmen wir theoretisch unendlich viele Stichproben einer Grundgesamtheit und berechnen für jede dieser Stichprobe die Varianz. Dann erhalten wir als Stichprobenkennwertverteilung eine Verteilung von Varianzen. Der durchschnittliche Wert all dieser Varianzen ist nun aber nicht gleich der Populationsvarianz σ2. Die Varianz ist daher keine erwartungstreue Schätzung der Populationsvarianz. Folgende Gesetzmäßigkeit lässt sich nachweisen:
![]()
Das heißt: Die Stichprobenvarianz verschätzt die Populationsvarianz um den Faktor (n-1)/n.
Um eine erwartungstreue Schätzung der Populationsvarianz zu bekommen, müssen wir nun lediglich die Stichprobenvarianz mit dem Faktor n / (n-1) multiplizieren, also:
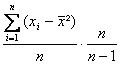
Wie man an der Formel leicht sieht, lässt sich das n herauskürzen. Um eine erwartungstreue Schätzung der Populationsvarianz zu erhalten, gehen wir also so vor:
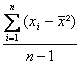
Neben der soeben ausführlicher erörterten Eigenschaft "erwartungstreu" werden an statistische Parameter auch noch die folgenden Anforderung gestellt. Sie sollten dazu noch sein: b) konsistent c) effizient
Ad b) Konsistent bedeutet: Erhöhen wir den Stichprobenumfang N, nähert sich der Stichprobenkennwert dem Populationskennwert. Diese Eigenschaft trifft sowohl auf den Mittelwert als auch auf die Varianz zu. Entnehmen wir eine Stichprobe mit dem gleichen Umfang wie die Population, so erhalten wir für diese spezielle Stichprobe einen Mittelwert von µ und eine Varianz von σ2. Der Umstand, dass sich der Stichprobenmittelwert bei großem N dem Mittelwert in der Population nähert, wird gelegentlich ebenfalls als Gesetz der großen Zahlen bezeichnet (vgl. Binomialverteilung).
Ad c) effizient gibt uns an, wie genau unser statistischer Kennwert den Kennwert in der Population schätzt. Diese Genauigkeit hängt ab von der Streuung der Stichprobenkennwerteverteilung. Ist diese Streuung klein, so haben wir einen relativ effizienten Stichprobenkennwert.
Wir haben nun alle wesentlichen Komponenten beschrieben, die wir benötigen, um die Stichprobenkennwertverteilung des Mittelwertes genauer untersuchen zu können.
Es sind vor allem drei wesentliche Eigenschaften, die bei der Verteilung der Stichprobenmittelwerte zu beachten sind:
1) erwartungstreu
2) Standardfehler des Mittelwertes
2) zentrales Grenzwerttheorem
ad 1) Wie wir bereits wissen, ist der Mittelwert eine erwartungstreue Schätzung des Populationsmittelwertes. Das bedeutet, dass der durchschnittliche Mittelwert über alle theoretisch erhobenen Stichproben gleich dem Populationsmittelwert ist. Heben wir diesen Umstand nochmals hervor:
Der Mittelwert der Stichprobenverteilung der Mittelwerte ist gleich dem Mittelwert der Population µ!
ad) 2) Die Streuung der Stichprobenverteilung der Mittelwerte wird als Standardfehler des Mittelwertes bezeichnet. Dies besagt: Jeder Stichprobenmittelwert ist eine Schätzung des Populationsmittelwertes. Der Standardfehler des Mittelwertes sagt uns nun etwas über die Genauigkeit dieser Schätzung. Ist der Standardfehler gering, so erhöht sich die Wahrscheinlichkeit, rein zufällig den 'wahren' Populationsmittelwert zu schätzen.
Dieser Standardfehler berechnet sich nun nach der Formel:
![]()
Wie wir aus der Formel erkennen können, besteht ein Zusammenhang zwischen dem Standardfehler des Mittelwertes, der Populationsvarianz und der Stichprobengröße.
Eine hohe Streuung in der Population bewirkt auch einen entsprechend hohen Standardfehler des Mittelwertes.
Umgekehrt gilt aber gleichfalls: Mit einer Erhöhung des Stichprobenumfangs N verringert sich der Standardfehler des Mittelwertes. Dies ist auch intuitiv einsichtig: Erheben wir im Extremfall Stichprobengrößen mit dem gleichen Umfang N wie die Gesamtpopulation, so wird der Mittelwert jeder dieser Stichproben gleich dem Populationsmittelwert sein. Die Streuung dieser Mittelwerte um den Populationsmittelwert ist gleich Null. Ist dagegen N = 1, so ist die Varianz der Stichprobenkennwerteverteilung gleich der Populationsvarianz!
ad 3) zentrales Grenzwerttheorem
Um Aussagen über die Wahrscheinlichkeit des Abweichens eines bestimmten empirisch erhobenen Mittelwertes vom Populationsmittelwert treffen zu können, müssen wir über die Verteilung der Stichprobenkennwerte bescheid wissen. Würden wir diese Verteilung von vornherein kennen, so können wir - vorausgesetzt Mittelwert und Varianz in der Population sind bekannt - die Wahrscheinlichkeit angeben, mit der ein bestimmter Mittelwert vom Populationsmittelwert abweicht.
Von großer Bedeutung hierbei ist das so genannte zentrale Grenzwerttheorem. Dieses besagt: Nehmen wir an, wir haben eine Population mit einem bestimmten µ und σ. Die Verteilung dieser Population sei aber unbekannt. Entnehmen wir dieser Population Stichproben mit zunehmendem N, so geht die Stichprobenkennwerteverteilung der Mittelwerte in eine Normalverteilung über. Wie man zeigen kann (vgl. Hays, 219f.), gilt dieser Umstand selbst im extremen Falle der Gleichverteilung der Populationsdaten!