Binomialverteilung
Unter Nützung der Regeln der Kombinatorik läßt sich nun eine der wichtigsten Verteilungen in der Wahrscheinlichkeitstheorie ermitteln: die Binomialverteilung, auch Bernoulli Verteilung genannt.
Jakob Bernoulli hat sich als erster mit folgenden Experimenten befaßt: Betrachten wir ein Experiment mit nur zwei möglichen Ausgängen. Wir haben es in diesem Falle also nur mit zwei Elementarereignissen zu tun. Beispiele: Das Werfen von Kopf oder Zahl bei einer Münze; das Würfel einer Sechs oder keiner Sechs bei einer Münze. Da es sich nur um zwei Elementarereignisse handelt, können wir das eine Elementarerignis auch als Erfolg und das zweite schlicht als Mißerfolg bezeichnen. Die Wahrscheinlichkeit des Erfolgs bezeichnet man als p und die Wahrscheinlichkeit für Mißerfolg als q. Die Wahrscheinlichkeit q = 1 -p, da die sich gegenseitig ausschließenden Ereignisse zusammengenommen das sichere Ereignis = 1 bilden. Dazu zwei Beispiele: Im Falle eines Münzwurfes ist p = 0.5 und q = 0.5; im Falle des Würfelns eines Sechsers ist p = 1/6 und q = 5/6.
Dieses Experiment wird nun n mal durchgeführt. Man bezeichnet eine derartige Versuchsreihe auch als Bernoulli-Prozeß.
Worum es nun konkret geht, ist die Frage, mit welcher Wahrscheinlichkeit bei insgesamt n Versuchen sich k-mal das Ereignis "Erfolg" einstellt. Eine typische Frage dafür ist also: Wie wahrscheinlich ist es, bei 5 Münzwürfen gerade 3 mal Erfolg (Erfolg sei beispielsweise Wappen) zu erzielen. Theoretisch ist es möglich, bei 5 Würfen von 0 bis zu 5 mal Wappen zu bekommen. Nun geht es also darum, dafür die verschiedenen Wahrscheinlichkeiten zu berechnen. Versuchen wir vorerst, für eine ganz spezielle Folge die Wahrscheinlichkeit zu berechnen. Nehmen wir an, wir hätten bei unserem Experiment das folgende Ergebnis erzielt: W, W, Z, Z, W (W bedeutet Wappen; Z bedeutet Zahl). Da die einzelnen Elementarereignis voneinander unabhängig sind und wir wissen wollen, mit welcher Wahrscheinlichkeit diese spezielle Folge von Elementarereignissen gemeisam auftritt, kommt hier das Multiplikationstheorem für unabhängige Ereignisse zum Tragen. Die Wahrscheinlichkeit für das Auftreten von "W, W, Z, Z, W" ist daher gleich p*p*q*q*p = 1/2^5.
Wir müssen allerdings daran denken, daß es sich hierbei um die Wahrscheinlichkeit für die spezielle Ereignisfolge "W, W, Z, Z, W" handelt. Was uns aber interessiert, ist die Wahrscheinlichkeit, 3 mal Wappen zu bekommen, u.zw. unabhängig davon, an welcher Stelle in der Ereignisfolge Wappen auftritt. Dreimal Wappen kann nun aber ingesamt in den folgenden verschiedenen Ereignisfolgen auftreten:
(Z, Z, W, W, W)
(Z, W, Z, W, W)
(Z, W, W, Z, W)
(Z, W, W, W, Z)
(W, Z, W, W, Z)
(W, Z, Z, W, W)
(W, Z, W, Z, W)
(W, W, Z, Z, W)
(W, W, Z, W, Z)
(W, W, W, Z, Z)
Da alle diese Ereignisfolgen voneinander unabhängig sind, kommt zur Berechnung der Gesamtwahrscheinlichkeit das Additionstheorem für voneinander unabhängige Ereignisse zum Tragen. Die Wahrscheinlichkeit, von 5 Würfen drei mal Wappen zu bekommen, beträgt daher: 10 * 1/2^3 * 1/2^2 = 10 * 1/2^5 = 0,3125
Statt die verschiedenen Vorkommnisse der Reihe nach auszuprobieren, ist es praktischer, dazu die Regel 3a (siehe Kombinatorik) - Kombinationen ohne Wiederholung - anzuwenden. Damit es einsichtig wird, warum hier gerade Regel 3a zur Anwendung kommt, überlegen wir uns das folgende: Zuerst numerieren wir die Ereignisfolge der Reihe nach durch. Dem ersten Münzwurf ordnen wir die Zahl 1 zu, dem zweiten die Zahl 2, usw. Bei fünf Münzwürfen erhalten wir auf diese Weise die fünf Zahlen 1,2,3,4,5. Aus diesen 5 Zahlen wählen wir drei Zahlen aus, die als Erfolg (was in unserem Beispiel Wappen bedeutet) bewertet werden. Damit kommt Regel 3a zur Anwendung:
![]()
Dies entspricht der Anzahl, die wir oben zunächst durch reines Ausprobieren gewonnen haben.
Die
Wahrscheinlichkeit, bei insgesamt 5 Münzwürfen 3 mal Wappen zu bekommen, beträgt daher: ![]() * 1/2^3 * 1/2^2
* 1/2^3 * 1/2^2
Ausgehend von dieser Formel können wir ganz analog dazu nun die Wahrscheinlichkeit dafür berechnen, bei insgesamt 5 Münzwürfen 0, 1, 2, 3, 4, 5-mal Wappen zu bekommen.
Das ergibt:
|
k |
P (k|5) = |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
Die Summe aller dieser 6 Wahrscheinlichkeiten ergibt 1!
Die allgemeine Formel zur Berechnung dieser Wahrscheinlickeiten ist:
![]()
Diese Berechnungsformel wird als Wahrscheinlichkeitsfunktion der Binomialverteilung bezeichnet.
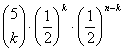
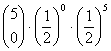 = 0.03125
= 0.03125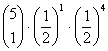 = 0.15625
= 0.15625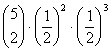 = 0.3125
= 0.3125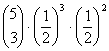 = 0.3125
= 0.3125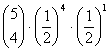 = 0.15625
= 0.15625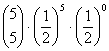 = 0.03125
= 0.03125