Verschiedene Binomialverteilungen und ihre Bedeutung für
die Inferenzstatistik
In dem einführenden Dokument zur Inferenzstatistik (ein „quickly prototyping“) wurde die Frage gestellt: Können wir bei einem Spieler, der bei beispielsweise 1000 Versuchen hintereinander einen 6er würfelt, noch länger an einen Zufall glauben? Wegen der Unwahrscheinlichkeit der Unschuldsbehauptung haben wir diese verworfen - die Wahrscheinlichkeit, 1000 mal hintereinander eine 6 zu würfeln, beträgt (1/6)1000 - und in dem Beispiel dem Spieler den weiteren Zugang zum Spielbetrieb verwehrt. Das Beispiel verfolgte freilich nur eine didaktische Zielsetzung: es sollte vorbereitend erläutert werden, dass die Unschuldsbehauptung (wir haben sie auch die Nullhypothese genannt) dann verworfen wird, wenn die für sie berechnete Wahrscheinlichkeit sehr gering ist.
Tatsächlich würden Sie im vorliegenden Falle eines Falschspielers nach anderen Kriterien vorgehen. Stellen Sie sich vor, Sie würden dem Spieler bei seiner Tätigkeit zuschauen. Würde er Ihnen auch dann verdächtig vorkommen, wenn er von 1000 Würfen 999-mal eine sechs würfelt? Oder nur 900-mal? Oder 850-mal? Vermutlich würden Sie in all den vier genannten Fällen einen Verdacht haben. Verdächtig ist der Spieler, wenn er also beispielsweise bei 1000-mal Würfeln 1000-mal, aber auch wenn er 999-mal, 900-mal und auch 850-mal eine sechs würfelt. Nicht die Einzelwahrscheinlichkeit dafür, gerade 1000-mal hintereinander eine sechs zu würfeln, ist für Sie ausschlaggebend, sondern die Wahrscheinlichkeit eines ganz Intervalls von verschiedenen Münzwürfen. Sie wollen beispielsweise wissen, wie wahrscheinlich ist es, 800-mal, 801-mal usw. bis 1000-mal bei 1000 Würfen eine sechs zu bekommen. Woran Sie also interessiert sind, ist die Frage, 800-mal oder mehr eine 6 zu würfeln. Die Wahrscheinlichkeit eines derartigen Intervalls bestimmen Sie mit Hilfe der Wahrscheinlichkeitsfunktion der Binomialverteilung. Sie wird auch als Überschreitungswahrscheinlichkeit bezeichnet.
Betrachten wir hierzu zwei kleine Beispiele von Binomialverteilungen:
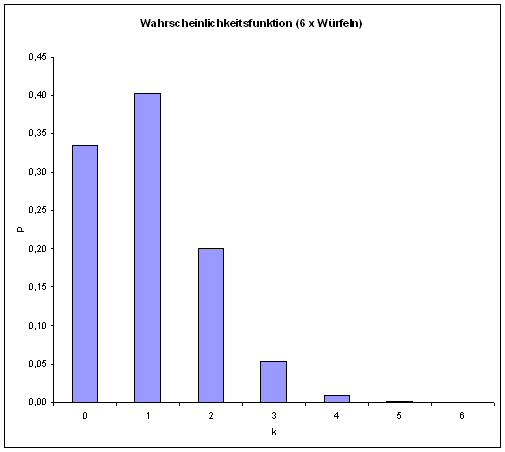
1) Die Wahrscheinlichkeitsfunktion der Binomialverteilung, bei 6-maligem Würfeln gerade k mal eine 6 zu bekommen
2) bei 4 Münzwürfen k mal Wappen zu bekommen
ad 1) n = 6; p =1/6; q =5/6
|
k |
P (k|6) = |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
Die Summe dieser Einzelwahrscheinlichkeiten ist, wie man leicht berechnen kann, 1!
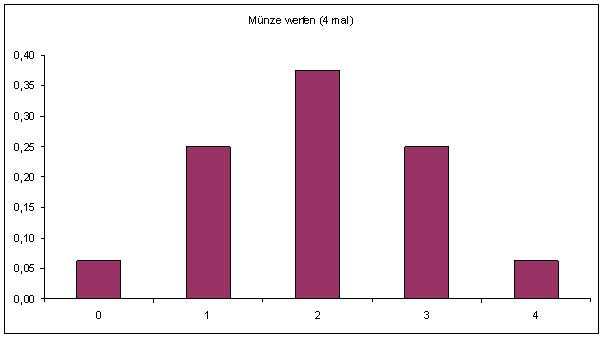
ad 2) bei 4 Münzwürfen k mal Wappen zu bekommen
n = 4; p=1/2; q=1/2
|
k |
P (k|4) = |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
Summe der P = 1!
Die letzten beiden Beispiele waren Beispiele für Bimonialverteilungen mit verschiedenem n und verschiedenem p. Die
allgemeine Formel
![]()
beschreibt also eine ganze Familie von Binomialverteilungen, abhängig von den Parametern n und p.
Wie berechnet man nun die Überschreitungswahrscheinlichkeit?
Wollen wir z.B. wissen, wie wahrscheinlich es ist, bei insgesamt 6-maligem Würfeln 5-mal oder mehr eine 6 zu bekommen, so lässt sich dies mit Hilfe der oben angegebenen Binomialverteilung (1. Beispiel) so berechnen: Wie zählen die Einzelwahrscheinlichkeiten für 5mal und 6mal eine 6 zu bekommen zusammen, also: 0.000643004 + 0.000021433 = 0,000664437
Das gleiche Ergebnis (bis auf Rundungsfehler) bekommen wir, indem wir die Einzelwahrscheinlichkeiten für 1mal, 2mal, 3mal und 4mal eine 6 zu würfeln aufaddieren (das ergibt in der Summe 0,999335562) und die erhaltene Summe dann von 1 (man beachte: die Summe aller Einzelwahrscheinlichkeiten beträgt 1) abziehen, nämlich: 1 – 0,999335562 = 0,000664438
Diese zwei verschiedenen Berechnungsarten der Überschreitungswahrscheinlichkeit werden wir bei Binomialverteilungen mit einem hohen n benötigen.
Wollen wir die Wahrscheinlichkeit dafür berechnen, bei 1000-maligem Würfeln 800 mal mehr eine 6 zu bekommen, so wird diese Berechnung mit Hilfe der Wahrscheinlichkeitsfunktion der Binomialverteilung ziemlich aufwändig:
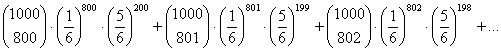
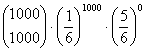
Was in einem solchen Falle zu tun ist, wird verständlicher, wenn wir uns zunächst bestimmte Eigenschaften der Binomialverteilung bei großem n näher ansehen.
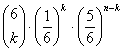
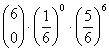 = 0.334897977
= 0.334897977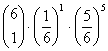 = 0.401877572
= 0.401877572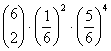 = 0.200938786
= 0.200938786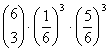 = 0.053583676
= 0.053583676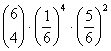 = 0.008037551
= 0.008037551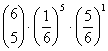 = 0.000643004
= 0.000643004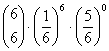 = 0.000021433
= 0.000021433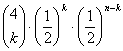
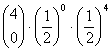 = 0.0625
= 0.0625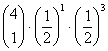 = 0.25
= 0.25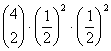 = 0.375
= 0.375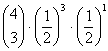 = 0.25
= 0.25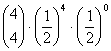 = 0.0625
= 0.0625