Leidlmair / Planung und statistische Auswertung psychologischer Untersuchungen I

Messtheoretische Vorüberlegungen

Am Anfang jeder statistischen Auswertung steht das 'Messen' bestimmter Phänomene bzw. Merkmale. Betrachten wir zunächst den folgenden, etwas vereinfacht dargestellten Messvorgang. In einer Schulklasse wurde das Geschlecht ermittelt. Dabei wurde an jedem der Schüler ein Schild angebracht mit den Zahlen 1 oder 2 (je nach Geschlecht). Auf dem gleichen Prinzip beruht auch eine Längenmessung: Wir ermitteln die Körper­größe von Schülern, indem wir sie an eine Meßlatte treten lassen und die abgelesene Zahl dem jeweiligen Schüler zuordnen. Diese simplen Beispiele zeigen, worauf das Messen letzten Endes hinausläuft: Messen ist eine Zuordnung von Zahlen zu Objekten (Probanden). Diese Behauptung ist freilich nur eine grobe Vereinfachung und keine brauchbare Definition. Will man sie präzisieren, so sind die mit dem Vorgang des Messens verbundenen Einzelschritte in der richtigen Reihenfolge zu untersuchen.

Zunächst werden bestimmte Merkmale für eine psychologische Untersuchung ausgewählt. Da sich pro Proband beliebig viele Merkmale feststellen lassen, ist es wichtig, vorerst die für die Untersuchung relevanten Merkmale auszuwählen (Beispiele: Geschlecht, Schulnoten, Körpergröße).

Für jedes der ausgewählten Merkmale kann pro Proband nur jeweils eine ­Merk­mals­ausprägung beobachtet werden (so wird beispielsweise beim Geschlecht pro Proband entweder die Merkmalsausprägung "männlich" oder "weiblich" festgestellt).

Für n Probanden erhalten wir - nach Beobachtung der Probanden - pro Merkmal n zugehörige Beobachtungseinheiten (= Merkmalsausprägungen von Probanden). Wir bezeichnen diese n verschiedenen Beobachtungseinheiten als die Menge der m(o_i), wobei der Index i den jeweiligen Probanden angibt (Beispiel: m(o₁) ist die Merkmalsau­sprägung des ersten Probanden hinsichtlich eines bestimmten Merkmals). Vergleicht man nun zwei beliebige Probanden o_i und o_j jeweils paarweise miteinander, so unter­scheiden sie sich in Bezug auf die beobachteten Merkmalsausprägungen m(o_i) und m(o_j). Die Bedeutung dieses Unterschieds bzw. die Kriterien, wodurch sich die Pro­banden hinsichtlich eines Merkmals unterscheiden, hängt allerdings vom jeweiligen Merkmal ab. So ist beim Geschlecht der einzig feststellbare Unterschied die Gleichheit bzw. Verschiedenheit der Probanden. Bei zwei Probanden o_i und o_j ist m(o_i) und m(o_j) entweder gleich oder eben ungleich. Das Merkmal Geschlecht führt daher zu einer Klassifikation der Probanden. Die Unterscheidung von Schülern im Hinblick auf Schulnoten führt dahingegen zu einer Ordnung der Schüler gemäß ihrer Leistung. Bei einem Vergleich zweier Schüler o_i und o_j lassen sich die zugehörigen Merkmalsausprägungen m(o_i) und m(o_j) in eine Rangordnung bringen.

In der Fachsprache bezeichnet man eine solche Menge von n Merkmalsausprägungen, durch die sich die Untersuchungsobjekte klassifizieren, ordnen oder auf andere Weise vergleichen lassen, als empirisches Relativ.

Verwendet man nun statt der Merkmalsausprägungen Zahlen (beispielsweise für die Schulnote 'sehr gut' die Zahl '1', für 'gut' die Zahl '2' usw.), so spricht man von einem numerischen Relativ.

Nun lassen sich nicht alle Beziehungen zwischen den Zahlen, die wir durch eine ausschließliche Betrachtung der Zahlen finden können, ohne Berücksichtigung deren Bedeutung auf die Merkmalsausprägungen des empirischen Relativs übertragen. So bedeutet beispielsweise die Zahl '4', wenn sie der Schulnote 'genügend' zugeordnet ist, keineswegs, dass der Schüler mit einer solchen Note doppelt so schlecht sein muss wie ein Schüler, der die Zahl '2' für 'gut' bekommen hat. Eine ähnliche Überlegung trifft auch auf die Ausprägungen für das Geschlecht zu, wenn wir diese mit '1' ('weiblich') und '2' ('männlich') codieren.

Je nachdem welche Beziehungen zwischen den Zahlen nun auch für die Merkmalsausprägungen des empirischen Relativs gelten, erhält man verschiedene Skalen. Man spricht von verschiedenen Skalenniveaus.  Die Frage nach dem jeweils vorliegenden Skalenniveau lässt sich nur emp­irisch beantworten. Die Antwort hängt - wie die Gegenüberstellung von 'Geschlecht' und 'Schulnoten' gezeigt hat - von den Eigenschaften des empirischen Relativs ab. Im Falle des Merkmals 'Geschlecht' ist beispielsweise die einzig relevante Beziehung zwischen den Zahlen im numerischen Relativ deren Gleichheit bzw. Verschiedenheit: Aus der Gleichheit bzw. Verschiedenheit der Zahlen im numerischen Relativ können wir auf eine entsprechende Gleichheit bzw. Verschiedenheit der Merkmalsausprägun­gen im empirischen Relativ schließen.

Ein weiteres wesentliches Grundproblem der Messtheorie ist die Frage, welche Veränderungen (Transformationen) der Skalenwerte auf einem bestimmten Skalenni­veau zulässig sind. Zulässig sind nur solche Veränderungen, bei denen auch nach durchgeführter Transformation das ursprüngliche Skalenniveau erhalten bleibt. Dieses Problem ist insofern wichtig, da wir ja mit den Skalenwerten statistische Operationen durchführen (beispielsweise - wenn erlaubt - die Bildung eines Mittelwertes). Durch diese statistischen Operationen werden aus den ursprünglichen Skalenwerten neue Werte berechnet. Soll das Skalenniveau nach der Rechenoperation erhalten bleiben, dann müssen auch die neu berechneten Werte die gleichen Beziehungen zwischen den Merkmalsausprägungen zum Ausdruck bringen wie die ursprünglichen Skalenwerte.

Verdeutlichen wir uns dies am Beispiel der Schulnotenskala. In diesem Falle ist jede Transformation - nennen wir sie T - zulässig, die folgende Bedingung erfüllt: Gilt für zwei ursprüngliche Skalenwerte die Beziehung  x > y, so müssen auch für die trans­formierten Werte T (x) und T (y) die Beziehung gelten T (x) > T (y). (So wäre bei­spielsweise auch die Zahlenfolge 1, 4, 9, 16, 17 eine gültige Schulnotenskala)

Intuitiv kann man sich dieses wichtige Problem der Messtheorie am Beispiel eines Flugsimulators veranschaulichen: Nur solche 'Operationen' am Flugsimulator sind zulässig, bei denen dessen Modellcharakter erhalten bleibt (drastisch ausgedrückt bedeutet dies: Operationen, die nur am Simulator durchführbar sind, beim konkreten Fliegen aber zu einem Absturz führen, sind nicht zulässig).

Vor dem Hintergrund dieser Überlegungen lassen sich nachstehende Skalentypen zusammenstellen. Für jede dieser Skalentypen sind insbesondere die drei Fragen zu beantworten: 1) Welche Beziehungen zwischen den Zahlen lassen sich auf das empirische Relativ übertragen? 2) Welche Veränderungen sind auf der jeweiligen Skala erlaubt? 3) Welche statistischen Operationen sind auf dem jeweiligen Skalenniveau erlaubt? Nach Beantwortung der drei Fragen werden in einem vierten Schritt erläuternde Beispiele angegeben.

 

 

Die Nominalskala

1) Berücksichtigte Relation

Bei der Nominalskala wird nur die Gleichheit bzw. Verschiedenheit der Zahlen voraus­gesetzt. Die Information, die sich aus dieser Relation herauslesen lässt, ist die Klassifikation der Probanden (sind die Zahlen gleich, so gehören die Probanden zur gleichen Gruppe; sind die Zahlen verschieden, so gehören die Probanden auch zu verschiedenen ­Grup­pen).

2) Erlaubte Transformationen

Erlaubt sind alle Transformationen, bei denen die in den ursprünglichen Skalenwerten enthaltene Information erhalten bleibt. Das bedeutet, dass nominalskalierte Werte in beliebige Zahlen transformiert werden können, sofern nur die aufgrund der ursprüngli­chen Skalenwerte getroffene Klassifikation der Probanden auch aus den transformierten Werten abgelesen werden kann.

Bei einer Nominalskala (Nomen, lat., bedeutet Benennung) dienen die Skalenwerte daher nur als Namen zur Identifikation der Klassenzugehörigkeit der Probanden. Jede Transformation, bei der die ursprüngliche Klasseneinteilung erhalten bleibt, führt ledig­lich zu einer Umbenennung der Klassen, zu einem anderen Codierschlüssel. Es können daher auch beliebige Zahlen verwendet werden, um die Probanden in verschiedene Klassen einzuteilen.

3) Erlaubte statistische Operationen

Die statistische Auswertung beschränkt sich bei der Nominalskala auf eine Auszählung. Man erhält Häufigkeitsverteilungen. Werden dabei mehrere Variablen berücksichtigt, so bekommt man mehrdimensionale Häufigkeitsverteilungen, so genannte Mehrfeldertafeln (Beispiel: Häufigkeitsverteilung des Geschlechts bezogen auf die Anteile der Raucher bzw. Nichtraucher in einem Kollektiv).

4) Beispiele für Nominalskala

Merkmal 'Geschlecht'

Merkmalsausprägungen	numerische Verschlüsselung
männlich	1
weiblich	2

 

Merkmal 'Haarfarbe'

Merkmalsausprägungen	numerische Verschlüsselung
schwarz	1
blond	2
braun	3
rot	4
usw.

 

Die Ordinalskala

1) Berücksichtigte Relation

Bei der Ordinalskala (ordo, lat., bedeutet Ordnung, Reihe) lässt sich aus der Ordnung der Zahlen (größer-kleiner-Relation) auf eine entsprechende Ordnung der Merkmalsausprägungen im empirischen Relativ schließen.

2) Erlaubte Transformationen

Erlaubt sind alle Transformationen, bei denen auch in den transformierten Werten die Rangordnung der ursprünglichen Zahlenwerte erhalten bleibt. Transformationen, bei denen die Rangordnung der Messwerte unverändert bleibt, bezeichnet man als monotone Transformationen. Monoton bedeutet, dass die Beziehung zwischen den ursprünglichen und den transformierten Rangzahlen kontinuierlich steigend oder fallend ist. Formal bedeutet dies: Gilt für zwei Messwerte x und y, dass x > y, so gilt auch für die trans­formierten Messwerte t(x) und t(y), dass t(x) > t(y). 

Man beachte aber, dass bei ordinalskalierten Messwerten der Abstand zwischen den Werten nicht definiert ist. Was dies in der Praxis heißt, sei an den folgenden drei Bei­spielen verdeutlicht:

a) Bei Schulnoten ist oft der Unterschied zwischen Rang 1 und Rang 2 wesentlich geringer als der Unterschied zwischen Rang 4 und 5. Numerisch gleiche Unterschiede (5 - 4 = 2 - 1) können also an verschiedenen Stellen der Skala ungleich groß sein.

b) Gelegentlich kommen bei einer Messung Werte vor, die mit dem Messinstrument nicht mehr erfasst werden können. Beispiele: höhere Geschwindigkeiten als auf dem Tachometer angegeben; größere Gewichte als auf der Waage erfassbar usw. Gibt ein Tachometer nur Geschwindigkeiten bis 200 km/h an, so werden höhere Geschwindig­keiten nur mehr insofern erkennbar, als das Messinstrument das oberste Ende der ange­gebenen Skala anzeigt (bzw., um im angegebenen Beispiel zu bleiben, die Tachonadel am oberen Messbereich ankommt). Von solchen speziellen Messungen können wir lediglich sagen, dass sie mindestens gleich groß oder größer sind als die maximal erfass­bare Messung, wir können aber nicht sagen, um wie viel größer. 205 Stundenkilometer ergeben beispielsweise den gleichen Messwert wie 300 Stundenkilometer. Will man auch diese Messungen für eine statistische Auswertung berücksichtigen (weil im vorlie­genden Experiment etwa nur wenige Messungen insgesamt verfügbar sind), so dürfen wir nur die ordinale Information der Messungen in Betracht ziehen. Da bei ordinalska­lierten Messwerten der Abstand zwischen den Werten nicht definiert ist, spielt bei diesen Messungen die Frage, um wie viel Maßeinheiten eine Messung größer ist als eine andere, keine Rolle.

c) Da auf Ordinalskalenniveau die Abstände zwischen den Messwerten nicht definiert sind, ist eine geometrisch-räumliche Darstellung von Distanzen zwischen den Messwer­ten nicht möglich. Das bedeutet, vereinfacht ausgedrückt, dass der Abstand von zwei - als Punkte in einem kartesischen Koordinatensystem - dargestellten Messwerte nicht als messbare Strecke interpretiert werden kann. Damit lässt sich die Verbindung zwischen den beiden Punkten nicht graphisch (etwa durch eine Linie) darstellen.

Ordinalskalierte Messwerte sind im strengen Sinne des Wortes keine Maßeinheiten. Das der Ordinalskala zugrunde liegende Messmodell beschreibt keine metrische Topolo­gie (topos, gr., bedeutet Ort). Worüber bei ordinalskalierten Messwerten keine Aussage möglich ist, zeigt das folgende - etwas futuristische - Beispiel:

Man stelle sich ein Universum vor, in dem die räumlichen Abstände zwischen den Himmelskörpern A, B und C nicht bestimmbar sind. Bekannt sei nur, dass B weiter entfernt ist als A und C weiter als B. Schickt man ein Raumschiff mit einer konstanten Geschwindigkeit zu diesen Himmelskörpern, so können wir nur die Reihenfolge wis­sen, in der es die Himmelskörper erreichen wird, nicht aber die Zeit.

3) Erlaubte statistische Operationen

Erlaubt sind alle statistische Verfahren, die nur die Rangfolge der Messwerte berücksichtigen.

4) Beispiele

Grade von Ängstlichkeit; Schulnoten; Sympathiewerte.

Alle Klassifikationen, bei denen nur die Reihenfolge der Zeichen festgelegt ist (z.B. schlecht, mittelmäßig, gut; sehr klein, klein, mittelgroß, groß, sehr groß).

 

 

Die Intervallskala

1) Berücksichtigte Relation

Bei der Intervallskala wird vorausgesetzt, dass numerisch gleiche Abstände zwischen den Messwerten an verschiedenen Stellen der Skala auch entsprechend gleiche Abstände zwischen den beobachteten Merkmalsausprägungen reflektieren. Man kann dies auch so formulieren: Die Größe des Unterschieds zwischen zwei intervallskalierten Messwerten ist eine abstandsgetreue Abbildung des tatsächlichen Unterschieds zwischen zwei empirisch gegebenen Merkmalsausprägungen. Erst ab Intervallskala haben wir es mit definierten Maßeinheiten zu tun. Die Intervallskala ist daher im engeren Sinne des Wortes erst eine metrische Skala. Intervallskalierte Messwerte sind nicht nur der Größe nach geordnet, sondern enthalten zusätzlich noch die Information, um wie viele Maßein­heiten sich ein Messwert von einem anderen unterscheidet.

2) Erlaubte Transformationen

Erlaubt sind Transformationen, bei denen die in der Intervallskala enthaltene Informati­on - gemeint sind die aus den Messwerten ablesbaren Abstände zwischen den Merkmalsausprägungen - erhalten bleibt. Dies sind alle linearen Transformationen. Es ist daher möglich, eine abstandsgetreue Abbildung in eine andere durch eine Lineartransformati­on umzuwandeln.

Beispiel: Umwandlung der Fahrenheit-Skala in Celsius (Formel: C° = (5/9) (F° - 32)). Betrachten wir zunächst die Temperatur gemessen an vier Tagen in Fahrenheit:

1. Tag: 60°; 2. Tag: 68°; 3. Tag: 71°; 4. Tag: 79°

Zwischen dem ersten und dem zweiten Tag und zwischen dem dritten und vierten Tag besteht der numerisch gleiche Temperaturunterschied, nämlich jeweils 8° Fahrenheit. Diese numerisch gleichen Abstände zwischen den beiden Messwertpaaren bedeuten nun - Intervallskala (!) - einen gleichen Temperaturunterschied zwischen den Tagen. Trans­formiert man nun diese Fahrenheit-Skala in Celsius, so bleibt diese Information erhal­ten:

1. Tag: 15,6°; 2. Tag: 20°; 3. Tag: 21,7°; 4. Tag: 26,1°

Wird die Temperatur statt in Fahrenheit in Celsius angegeben, so lässt sich daraus der gleiche Unterschied zwischen den Tagen 1 und 2 und den Tagen 3 und 4 ablesen, nämlich jeweils 4,4 C°.

3) Erlaubte statistische Operationen

Da zu den linearen Transformationen die Rechenoperationen Addieren, Subtrahieren, Multiplizieren und Dividieren gehören, können auf Intervallskalenniveau Mittelwert und Streuungsmaße (Varianz) berechnet werden. Beide Maße sind wesentliche Bausteine für viele Verfahren in der (parametergebundenen) Statistik.

4) Beispiele

Temperaturskalen; kalendarische Jahreszahlen; Uhrzeiten

 

 

Die Verhältnisskala (Proportionalskala)

Da die Verhältnisskala eher in den Naturwissenschaften, speziell in der Physik, vor­kommt und da die meisten in der Psychologie verwendeten statistischen Verfahren bereits mit intervallskalierten Messwerten durchgeführt werden können, wird auf sie nur kurz eingegangen.

1) Berücksichtigte Relation: Die Verhältnisskala ist eine quotientengetreue Abbildung von zwei empirisch gegebenen Merkmalsausprägungen. Das bedeutet: Ist ein Messwert a numerisch doppelt so groß wie ein Messwert b, so entspricht dies den tatsächlichen Verhältnissen (= Proportionen) der Merkmalsausprägungen im empirischen Relativ. So lässt sich beispielsweise aus den beiden numerischen Altersangaben 40 und 20 auf ein entsprechendes ­Al­ters­verhältnis zwischen den Probanden schließen. Voraussetzung für die Verhältnisskala ist das Vorhandensein eines absoluten Nullpunktes.

Man kann sich diese Voraussetzung am Beispiel der (intervallskalierten) Celsius Skala verdeutlichen. So bedeutet etwa 40° C keine Verdoppelung der Wärme gegenüber 20° C. Der Nullpunkt der Celsius Skala ist willkürlich festgesetzt (Gefrierpunkt des Was­sers). Der absolute Nullpunkt liegt bei -273° C. Die Strecke von 40° C zu -273° C ist aber nicht das doppelte der Strecke von 20° C zu -273° C. Daher ist die Celsius Skala intervallskaliert, nicht jedoch verhältnisskaliert. Verdeutlichen wir uns diesen Umstand am Beispiel der folgenden Graphik:

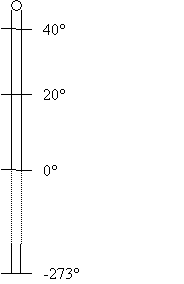
2) Einzig erlaubte Transformation bei der Verhältnisskala (erlaubt heißt: das ursprüng­liche Quotientenverhältnis der Messwerte bleibt auch bei den transformierten Werten erhalten) ist ein multiplikativer Faktor (y = b x; wobei b > 0).

 

 

Abschließende Bemerkungen

 1) Die vier beschriebenen Skalentypen - Nominalskala, Ordinalskala, Intervallskala, Verhältnisskala - wurden in der Reihenfolge ihrer Wertigkeit angeführt, wobei die Nominalskala die niederwertigste Skala und die Verhältnisskala die hochwertigste Skala ist.  Wichtig ist der folgende Umstand:

Der jeweils höherwertigere Skalentyp erbt die Eigenschaften aller niederwertigeren Skalentypen. So wird beispielsweise bei der Intervallskala auch die bei der Ordinalskala und der Nominalskala jeweils berücksichtigte Relation vorausgesetzt (bei intervallska­lierten Werten kann aus der Ordnung der Zahlen auf eine entsprechende Ordnung der Eigenschaftsausprägungen geschlossen werden - Ordinalskala! - und gleiche (bzw. verschiedene) Messwerte reflektieren gleiche (bzw. verschiedene) Merkmalsausprägun­gen - Nominalskala!).

2) Die hier beschriebenen messtheoretischen Voraussetzungen für statistische Anwen­dungen verstehen sich lediglich als 'Wenn-dann'-Bedingungen. Sie enthalten keine Anweisungen darüber, welche statistischen Verfahren in einer bestimmten Untersu­chung erlaubt sind. Die Antwort auf diese Frage hängt vom jeweiligen Skalenniveau ab. Welches Skalenniveau angemessen ist, darüber hat ausschließlich der Psychologe - und eben nicht: der Statistiker - zu befinden.

Wird daher bei einer Untersuchung ein falscher Test eingesetzt, so ist dafür auch allein der Anwender verantwortlich. Nicht die Rechenverfahren als solche sind falsch, sondern deren Anwendung unter falschen inhaltlichen Voraussetzungen. Die Statistik rechnet mit 'Zahlen' und diese Zahlen als solche geben uns keine Auskunft darüber, auf welchem Skalenniveau die Messwerte angesiedelt sind. Gerade deswegen sind Fehler bei der Interpretation der 'Zahlen' gravierend. So ist beispielsweise zu fragen, inwie­fern subjektiv empfundene 'Distanzen' (man denke etwa an Sympathiewerte) als geome­trisch-räumliche Distanzen aufgefasst werden können. 'Rechnet' man mit derartigen Distanzen als wären sie intervallskaliert, so unterschiebt man unter Umständen den tatsächlichen Werten ein falsches Modell und kommt dergestalt zu falschen Rückschlüs­sen über die Beziehungen in der realen Welt. Dies zu entscheiden ist jedoch, wie be­reits erwähnt, Aufgabe des Psychologen und nicht des Statistikers.